题目内容
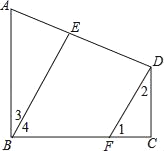
【题目】如图，已知AB=AC，将BC沿BD所在的直线折叠，使点C落在AB边上的E点处．
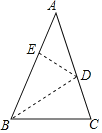
(1)若∠ADE=30°，求∠BDC的度数．
(2)若AB=AC=8，BC=5，求三角形AED的周长．
【答案】(1)∠BDC=75°；(2)11.
【解析】
(1)依据折叠的性质，即可得到∠BDC=
(180°-∠ADE)=75°；
(2)依据折叠可得，BC=BE=5，CD=ED，AB=AC=5，即可得到AE=AB-BE=3，进而得出三角形AED的周长=AD+DE+AE．
解：(1)∵∠BDC=∠BDE，∠ADE=30°，
∴∠BDC=(180°-30°)=75°；
(2)∵BC=BE=5，CD=ED，AB=AC=5，
∴AE=AB-BE=8-5=3．
∴三角形AED的周长=AD+DE+AE=AC+3=8+3=11．
练习册系列答案
阅读快车系列答案
相关题目
