Question

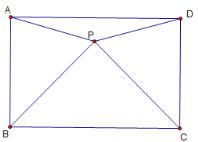
【题目】如图，P 为平行四边形 ABCD 内一点，PB=PC，∠BPC=90°，∠PAB=75°，若 AB=11，PD=14，则 PA 的长为_______________．

Answer 1

【答案】

【解析】

根据等腰直角三角形BPC得到∠BPC=90°，再根据矩形的性质得到△ABE是等腰直角三角形，在Rt△ABE中求得AE的长，最后在Rt△AEP中求得AP的长.

如下图,过点A作BP的垂线，交BP于点E

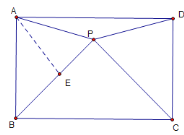
∵BP=CP，∠BPC=90°

∴∠PBC=45°

∵四边形ABCD是矩形，∴∠ABC=90°

∴∠ABP=45°

∵AE⊥BP，∴△ABE是等腰直角三角形

∵AB=，∴在Rt△ABE中，BE=AE==11

∵∠BAP=75°，∴∠EAP=30°

∴在Rt△AEP中，EP==，AP=2×=

故答案为：