Question

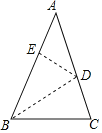
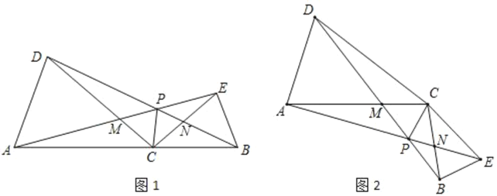
【题目】如图1，点C为线段AB上任意一点（不与点A、B重合），分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE，CA＝CD，CB＝CE，∠ACD＝∠BCE＝30°，连接AE交CD于点M，连接BD交CE于点N，AE与BD交于点P，连接CP．

（1）线段AE与DB的数量关系为　 ；请直接写出∠APD＝　 ；

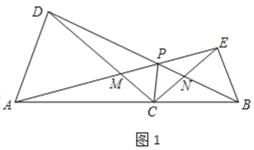
（2）将△BCE绕点C旋转到如图2所示的位置，其他条件不变，探究线段AE与DB的数量关系，并说明理由；求出此时∠APD的度数；

（3）在（2）的条件下求证：∠APC＝∠BPC．

Answer 1

【答案】（1）AE＝BD，30°；（2）结论：AE＝BD，∠APD＝30°．理由见解析；（3）见解析.

【解析】

（1）只要证明△ACE≌△DCB，即可解决问题；
（2）只要证明△ACE≌△DCB，即可解决问题；
（3）如图2-1中，分别过C作CH⊥AE，垂足为H，过点C作CG⊥BD，垂足为G，利用面积法证明CG=CH，再利用角平分线的判定定理证明∠DPC=∠EPC即可解决问题；

（1）解：如图1中，

∵∠ACD＝∠BCE，

∴∠ACD+∠DCE＝∠BCE+∠DCE，

∴∠ACE＝∠DCB，

又∵CA＝CD，CE＝CB，

∴△ACE≌△DCB．

∴AE＝BD，∴CAE＝∠CDB，

∵∠AMC＝∠DMP，

∴∠APD＝∠ACD＝30°，

故答案为AE＝BD，30°

（2）如图2中，结论：AE＝BD，∠APD＝30°．

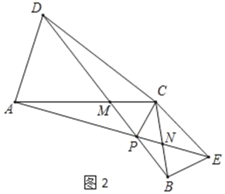
理由：∵∠ACD＝∠BCE，

∴∠ACD+∠DCE＝∠BCE+∠DCE，

∴∠ACE＝∠DCB，

又∵CA＝CD，CE＝CB，

∴△ACE≌△DCB．

∴AE＝BD，∴CAE＝∠CDB，

∵∠AMP＝∠DMC，

∴∠APD＝∠ACD＝30°．

（3）如图2﹣1中，分别过C作CH⊥AE，垂足为H，过点C作CG⊥BD，垂足为G，

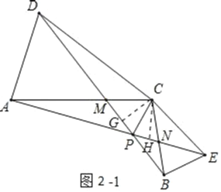
∵△ACE≌△DCB．

∴AE＝BD，

∵S△ACE＝S△DCB

∴CH＝CG，

∴∠DPC＝∠EPC

∵∠APD＝∠BPE，

∴∠APC＝∠BPC．