题目内容
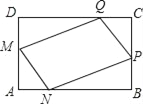
【题目】为了美化环境,学校准备在如图所示的矩形ABCD空地上进行绿化,规划在中间的一块四边形MNQP上种花,其余的四块三角形上铺设草坪,要求AM=AN=CP=CQ,已知BC=24米,AB=40米,设AN=x米,种花的面积为y1平方米,草坪面积y2平方米.
(1)分别求y1和y2与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当AN的长为多少米时,种花的面积为440平方米?
(3)若种花每平方米需200元,铺设草坪每平方米需100元,现设计要求种花的面积不大于440平方米,设学校所需费用W(元),求W与x之间的函数关系式,并求出学校所需费用的最大值.
【答案】(1)y2=2x2﹣64x+960,y1=﹣2x2+64x;(2)10米或22米;
(3)W=﹣200(x﹣16)2+147200,最大值为140000元.
【解析】试题分析:(1)根据三角形面积公式可得y2的解析式,再用长方形面积减去四个三角形面积,即可得y1的函数解析式;
(2)根据题意知y1=440,即即可得关于x的方程,解方程即可得;
(3)列出总费用的函数解析式,将其配方成顶点式,根据花的面积不大于440平方米可得x的范围,结合此范围根据二次函数性质即可得函数的最大值,从而得解.
试题解析:(1)根据题意,y2=2×![]() ×x×x+2×
×x×x+2×![]() (40﹣x)(24﹣x)=2x2﹣64x+960,
(40﹣x)(24﹣x)=2x2﹣64x+960,
y1=40×24﹣y2=﹣2x2+64x;
(2)根据题意,知y1=440,即﹣2x2+64x=440,
解得:x1=10,x2=22,
故当AN的长为10米或22米时种花的面积为440平方米;
(3)设总费用为W元,
则W=200(﹣2x2+64x)+100(2x2﹣64x+960)=﹣200(x﹣16)2+147200,
由(2)知当0<x≤10或22≤x≤24时,y1≤440,
在W=﹣200(x﹣16)2+147200中,当x<16时,W随x的增大而增大,当x>16时,W随x的增大而减小,
∴当x=10时,W取得最大值,最大值W=140000,
当x=22时,W取得最大值,最大值W=140000,
∴学校所需费用的最大值为140000元.