题目内容
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,则∠AOC= .
如图(2)若∠BOD=35°,则∠AOC= .
(2)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(3)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直.(填空)
(3) 当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .

【答案】(1)145,145;(2)详见解析;(3)详见解析.
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD-∠BOD可计算出∠AOC的度数;根据∠AOC=360°-∠BOD-∠AOB-∠COD可计算出∠AOC的度数;(2)由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补;(3)分别利用OD⊥AB、CD⊥OB、CD⊥AB、OC⊥AB分别求出即可.
解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°;
如图2,若∠BOD=35°,
则∠AOC=360°-∠BOD-∠AOB-∠COD
=360°-35°-90°-90°
=145°;
(2)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
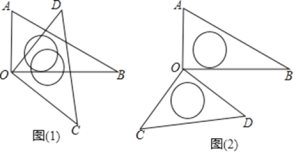
(3) 当 AB ⊥ OD 时,∠AOD = 30° .
当 CD ⊥ OA 时,∠AOD = 45° .
当 OC ⊥ AB 时,∠AOD = 60° .
当 AB ⊥ CD 时,∠AOD = 75° .
即∠AOD角度所有可能的值为:30°、45°、60°、75°.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案