Question

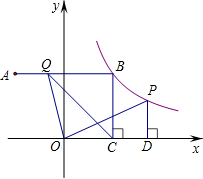
在平面直角坐标系中，点A（-3，4）关于y轴的对称点为点B，连接AB，反比例函数y=

k

x

（x＞0）的图象经过点B，过点B作BC⊥x轴于点C，点P是该反比例函数图象上任意一点，过点P作PD⊥x轴于点D，点Q是线段AB上任意一点，连接OQ、CQ．
（1）求k的值；
（2）判断△QOC与△POD的面积是否相等，并说明理由．

Answer 1

（1）∵点B与点A关于y轴对称，A（-3，4），
∴点B的坐标为（3，4），
∵反比例函数y=

k

x

（x＞0）的图象经过点B．
∴

k

3

=4，
解得k=12．

（2）相等．理由如下：
设点P的坐标为（m，n），其中m＞0，n＞0，
∵点P在反比例函数y=

12

x

（x＞0）的图象上，
∴n=

12

m

，即mn=12．
∴S_△POD=

1

2

OD•PD=

1

2

mn=

1

2

×12=6，
∵A（-3，4），B（3，4），
∴AB∥x轴，OC=3，BC=4，
∵点Q在线段AB上，
∴S_△QOC=

1

2

OC•BC=

1

2

×3×4=6．
∴S_△QOC=S_△POD．