Question

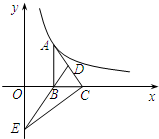
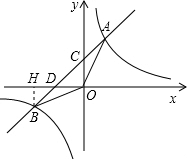
已知：如图，一次函数的图象经过第一、二、三象限，且与反比例函数的图象交于A、B两点，与y轴交于点C，与x轴交于点D．OB=

10

，tan∠DOB=

1

3

．
（1）求反比例函数的解析式；
（2）设点A的横坐标为m，求m的取值范围．

Answer 1

（1）过点B作BH⊥x轴于点H，
在Rt△OHB中，HO=3BH，
由勾股定理，得BH²+HO²=OB²，
又∵OB=

10

，
∴BH²+（3BH）²=（

10

）²，
∵BH＞0，
∴BH=1，HO=3，
∴点B（-3，-1），
设反比例函数的解析式为y=

k1

x

（k≠0），
∵点B在反比例函数的图象上，代入得：k₁=3，
∴反比例函数的解析式为y=

3

x

．
答：反比例函数的解析式为y=

3

x

．

（2）设直线AB的解析式为y=k₂x+b（k≠0）．　　
由点A在第一象限，得m＞0，
又由点A在函数y=

3

x

的图象上，可求得点A的纵坐标为

3

m

，
∵点B（-3，-1），点A（m，

3

m

），
∴

-3k2+b=-1 mk2+b= 3 m

解关于k₂、b的方程组，得

k2= 1 m b= 3-m m

，
∴直线AB的解析式为　y=

1

m

x+

3-m

m

，
由已知，直线经过第一、二、三象限，
∴b＞0时，即　

3-m

m

＞0，
∵m＞0，
∴3-m＞0，
由此得　0＜m＜3．
答：m的取值范围是0＜m＜3．