Question

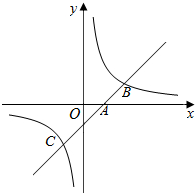
如图，一次函数y=-x-1与反比例函数y=

m

x

交于第二象限点A．一次函数y=-x-1与坐标轴分别交于B、C两点，连接AO，若tan∠AOB=

1

3

．
（1）求反比例函数的解析式；
（2）求△AOC的面积．

Answer 1

（1）设A（a，b），结合题意，
-a-1=b，
又tan∠AOB=

1

3

，
即有3b+a=0；
可得出a=-

3

2

，b=

1

2

；
即A（-

3

2

，

1

2

），
代入反比例函数解析式中，有

1

2

=

m

- 3 2

，
得m=-

3

4

，
故反比例函数解析式为：y=-

3

4x

；

（2）因为一次函数y=-x-1与坐标轴交C点，
令x=0，得y=-1，
即C（0，-1）；
所以OC=1；
又∵A（-

3

2

，

1

2

），
即点A到x轴的距离为

1

2

，
因为一次函数y=-x-1与x轴交B点，
令y=0，得x=-1，
即B（-1，0）；
则OB=1，
所以S_△AOC=

1

2

OB•

1

2

+

1

2

OB•OC=

3

4

；