Question

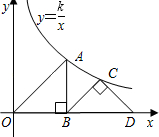
如图，已知双曲线y=

k

x

（x＞0）经过矩形OABC的边AB、BC上的点F、E，其中CE=

1

3

CB，AF=

1

3

AB，且四边形OEBF的面积为2，则k的值为______．

Answer 1

设矩形的长为a，宽为b，
则由CE=

1

3

CB，AF=

1

3

AB，得：
CE=

1

3

a，AF=

1

3

b，
∴三角形COE的面积为：

1

6

ab，
三角形AOF的面积为：

1

6

ab，
矩形的面积为：ab，
四边形OEBF的面积为：ab-

1

6

ab-

1

6

ab=

2

3

ab，
∴

三角形AOF的面积

四边形OEBF的面积

=

1 6

2 3

，
∴三角形AOF的面积=四边形OEBF的面积×

1

4

=2×

1

4

=

1

2

，
∴

1

2

|k|=

1

2

，
又由于反比例函数的图象位于第一象限，k＞0；
∴k=1．
故答案为：1．