题目内容
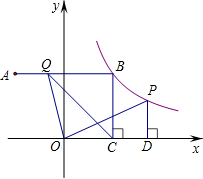
如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数y=
的图象经过D、E两点,则点E的坐标是______;点D的坐标是______;△DOE的面积为______.
| 4 |
| x |

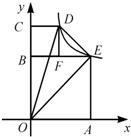
∵四边形AOBE,∴AO=AE,
设AO=a,则点E为(a,a)
∴
=a,整理得a2=4,
解得a=2,a=-2(舍去),
所以点E的坐标是(2,2),
设正方形CBFD的边长为b,则BF=b,CO=2+b,
所以点D为(b,2+b),
∴
=2+b,整理得b2+2b-4=0,
解得b=
-1,b=-
-1(舍去),
所以点D的坐标是(
-1,
+1);
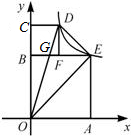
设直线OD与BE的交点为G,则点G的纵坐标为2,
直线OD的解析式为y=
x,即y=
x,
∴
x=2,
解得x=3-
,
∴EG=2-(3-
)=
-1,
所以S△DOE=S△OEG+S△DEG=
×EG×OB+
×EG×BC
=
×(
-1)×2+
×(
-1)×(
-1)
=2.
设AO=a,则点E为(a,a)
∴
| 4 |
| a |
解得a=2,a=-2(舍去),
所以点E的坐标是(2,2),
设正方形CBFD的边长为b,则BF=b,CO=2+b,
所以点D为(b,2+b),
∴
| 4 |
| b |
解得b=
| 5 |
| 5 |
所以点D的坐标是(
| 5 |
| 5 |

设直线OD与BE的交点为G,则点G的纵坐标为2,
直线OD的解析式为y=
| ||
|
3+
| ||
| 2 |
∴
3+
| ||
| 2 |
解得x=3-
| 5 |
∴EG=2-(3-
| 5 |
| 5 |
所以S△DOE=S△OEG+S△DEG=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
=2.

练习册系列答案
相关题目

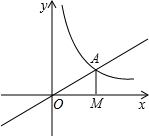
 OB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=
OB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=