��Ŀ����
ij���̻�е�������г����ƻ�����A��B�����ͺŵĴ����ھ����100̨���ó����������ʽ�����22 400��Ԫ����������22 500��Ԫ���������ʽ�ȫ�����������������ھ�����������Ĵ������ھ����ȫ���۳����������ھ���������ɱ����ۼ����±���
| �ͺ� | A | B |
| �ɱ�����Ԫ/̨�� | 200 | 240 |
| �ۼۣ���Ԫ/̨�� | 250 | 300 |
��2���ó���������ܻ���������
��3�������г����飬ÿ̨B���ھ�����ۼ۲���ı䣬ÿ̨A���ھ�����ۼ۽������m��Ԫ��m��0�����ó�Ӧ�������������������ע������=�ۼ۩��ɱ���
�⣺��1��������A���ھ��x̨����B���ھ����100��x��̨��
�������22400��200x+240��100��x����22500�����37.5��x��40��
��xȡ�Ǹ���������xΪ38��39��40��
������������������
��A��38̨��B��62̨��
��A��39̨��B��61̨��
��A��40̨��B��60̨��
��2����������W����Ԫ�����������W=50x+60��100��x��=6000��10x��
�ߩ�10��0����W��x���������С��
�൱x=38ʱ��W���=5620����Ԫ����
������A��38̨��B��62̨ʱ������������
��3���������W=��50+m��x+60��100��x��=6000+��m��10��x
�൱0��m��10����x=38ʱ��W�������A��38̨��B��62̨��
��m=10ʱ��m��10=0�����������������������ȣ�
��m��10����x=40ʱ��W�������A��40̨��B��60̨��
����

��ϰ��ϵ�д�
 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
�����Ŀ
 ��ͼ��ֱ��PB��һ�κ���
��ͼ��ֱ��PB��һ�κ��� ��ͼ��
��ͼ��
 �����߶�AE����ֱ�ߵĽ���ʽ��
�����߶�AE����ֱ�ߵĽ���ʽ�� (Сʱ)��һ�κ�����ij����������ʱ������������������ʻʱ��ı仯��ϵ��ͼ��
(Сʱ)��һ�κ�����ij����������ʱ������������������ʻʱ��ı仯��ϵ��ͼ��

 ����C����������18��0��.
����C����������18��0��.
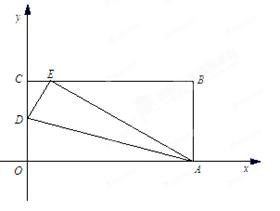
 ��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B��P������BO�ϵ�һ�����㣨��P�����B�غϣ�������P��PC��AB������ΪC��������CA�Ͻ�ȡCD=CP������PD����BP=t��
��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B��P������BO�ϵ�һ�����㣨��P�����B�غϣ�������P��PC��AB������ΪC��������CA�Ͻ�ȡCD=CP������PD����BP=t��
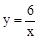 ��ͼ����һ�κ���y=kx+b��ͼ���ཻ������A��m��3����B����3��n����
��ͼ����һ�κ���y=kx+b��ͼ���ཻ������A��m��3����B����3��n����