如图.反比例函数的图象与一次函数y=kx+b的图象相交于两点A．(1)求一次函数的表达式,(2)观察图象.直接写出使反比例函数值大于一次函数值的自变量x的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

如图，反比例函数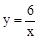的图象与一次函数y=kx+b的图象相交于两点A（m，3）和B（﹣3，n）．

（1）求一次函数的表达式；
（2）观察图象，直接写出使反比例函数值大于一次函数值的自变量x的取值范围．

（1）y=x+1
（2）x＜﹣3或0＜x＜2

解析分析：（1）将A与B坐标分别代入反比例解析式求出m与n的值，确定出A与B坐标，再将两点代入一次函数解析式中求出k与b的值，即可确定出一次函数解析式。
（2）由A与B的横坐标，利用函数图象即可求出满足题意x的范围。
解：（1）将A（m，3），B（﹣3，n）分别代入反比例解析式得：，
解得：m=2，n=﹣2。
∴A（2，3），B（﹣3，﹣2）。
将A与B代入一次函数解析式得：，解得：。
∴一次函数解析式为y=x+1。
（2）∵A（2，3），B（﹣3，﹣2），
∴由函数图象得：反比例函数值大于一次函数值的自变量x的取值范围为x＜﹣3或0＜x＜2。

练习册系列答案

相关题目

某工程机械厂根据市场需求，计划生产A、B两种型号的大型挖掘机共100台，该厂所筹生产资金不少于22 400万元，但不超过22 500万元，且所筹资金全部用于生产此两型挖掘机，所生产的此两型挖掘机可全部售出，此两型挖掘机的生产成本和售价如下表：

型号	A	B
成本（万元/台）	200	240
售价（万元/台）	250	300

（1）该厂对这两型挖掘机有哪几种生产方案？
（2）该厂如何生产能获得最大利润？
（3）根据市场调查，每台B型挖掘机的售价不会改变，每台A型挖掘机的售价将会提高m万元（m＞0），该厂应该如何生产获得最大利润？（注：利润=售价﹣成本）

在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时x（h）之间的函数图象，根据图象解答以下问题：

（1）写出A、B两地直接的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义；
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．

某公司投资700万元购甲、乙两种产品的生产技术和设备后，进行这两种产品加工．已知生产甲种产品每件还需成本费30元，生产乙种产品每件还需成本费20元．经市场调研发现：甲种产品的销售单价为x（元），年销售量为y（万件），当35≤x＜50时，y与x之间的函数关系式为y=20﹣0.2x；当50≤x≤70时，y与x的函数关系式如图所示，乙种产品的销售单价，在25元（含）到45元（含）之间，且年销售量稳定在10万件．物价部门规定这两种产品的销售单价之和为90元．

（1）当50≤x≤70时，求出甲种产品的年销售量y（万元）与x（元）之间的函数关系式．
（2）若公司第一年的年销售量利润（年销售利润=年销售收入﹣生产成本）为W（万元），那么怎样定价，可使第一年的年销售利润最大？最大年销售利润是多少？
（3）第二年公司可重新对产品进行定价，在（2）的条件下，并要求甲种产品的销售单价x（元）在50≤x≤70范围内，该公司希望到第二年年底，两年的总盈利（总盈利=两年的年销售利润之和﹣投资成本）不低于85万元．请直接写出第二年乙种产品的销售单价m（元）的范围．

甲、乙两车分别从A，B两地同时出发相向而行．并以各自的速度匀速行驶，甲车途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．
（1）直接写出a，m，n的值；
（2）求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；
（3）当两车相距120千米时，乙车行驶了多长时间？