题目内容
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,若△ECD的周长为2,△EBA的周长为6.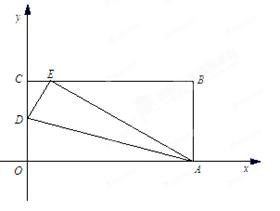
(1)矩形OABC的周长为 ;
(2)若A点坐标为 ,求线段AE所在直线的解析式.
,求线段AE所在直线的解析式.
(1)8;(2)直线AE的解析式为y= x+
x+ .
.
解析试题分析:(1)由折叠的意义,△ECD的周长与△EBA的周长之和等于矩形OABC的周长,
(2)根据A点坐标为(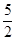 ,0),求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.
,0),求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.
试题解析:
解:(1)∵DE=DO,EA=OA,
∴矩形OABC的周长=△ECD的周长+△EBA的周长.
∴矩形OABC的周长为8.
(2)∵OA=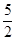 ,
,
∴AB=OC=
∴BE=6? ?
?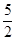 =2
=2
∴CE=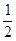 ,即点E的坐标为(
,即点E的坐标为(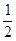 ,
, )
)
设直线AE的解析式为y=kx+b,
则 解得
解得 ,
,
∴直线AE的解析式为y= x+
x+ .
.
考点:一次函数综合题.

练习册系列答案
相关题目
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价﹣成本)
 ,
, 为何值时,它的图象经过原点;
为何值时,它的图象经过原点; ).
). ,第一批产品
,第一批产品
 与上市时间的关系式;
与上市时间的关系式;
 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小?
 x的图象相交于点(2,a)。
x的图象相交于点(2,a)。
