题目内容
如图,直线PA是一次函数 的图象,直线PB是一次函数
的图象,直线PB是一次函数 的图象.
的图象.
(1)求A、B、P三点的坐标;(2)求四边形PQOB的面积;
(1)A(-1,0),B(1,0),
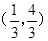 ;(2)
;(2)
解析试题分析:本题考查了一次函数综合题,难度一般,关键是掌握把四边形的面积分成两个三角形面积的差进行求解.(1)令一次函数y=x+1与一次函数y=-2x+2的y=0可分别求出A,B的坐标,再由 y=x+1和 y=?2x+2 构建二元一次方程组,可求出点P的坐标;
(2)根据四边形PQOB的面积=S△BOM-S△QPM即可求解.
试题解析:
解:(1)∵一次函数y=x+1的图象与x轴交于点A,
∴A(-1,0),
∵一次函数y=-2x+2的图象与x轴交于点B,
∴B(1,0),
∵一次函数y=x+1的图象与一次函数y=-2x+2的图象交与点P
∴ 解得:
解得:
∴点P的坐标是: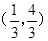
(2)∵直线PA与y轴交于点Q,则Q(0,1),设直线PB与y轴交于点M,则M(0,2),
∴

 .
.
考点:一次函数综合题.

练习册系列答案
相关题目
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22 400万元,但不超过22 500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
| 型号 | A | B |
| 成本(万元/台) | 200 | 240 |
| 售价(万元/台) | 250 | 300 |
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产获得最大利润?(注:利润=售价﹣成本)
 ,
, 为何值时,它的图象经过原点;
为何值时,它的图象经过原点; ).
). (元)与销售量
(元)与销售量 (支)之间的函数关系式;
(支)之间的函数关系式; (元)与销售量
(元)与销售量 +2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.
+2与x轴、y轴分别交于A、B两点,以AB为边在第二象限内作正方形ABCD.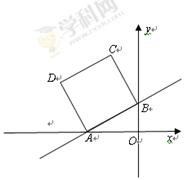
 ,第一批产品
,第一批产品
 与上市时间的关系式;
与上市时间的关系式;
 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小?