题目内容
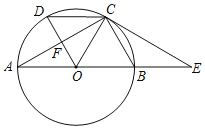
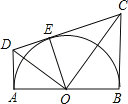
【题目】如图,AB为半圆O的直径,AD、BC分别与⊙O相切于点A,B,CD与⊙O相切于点E,AD与CD相交于D,BC与CD相交于C,连接OD、OE、OC,已知AD=2,BC=4,对于下列结论:①AD+BC=CD:②∠DOC=90°;③S梯形ABCD=![]() CDOA:④OA=2
CDOA:④OA=2![]() .其中结论正确的有_____.(请把正确的结论的序号填在横线上)
.其中结论正确的有_____.(请把正确的结论的序号填在横线上)
【答案】①②
【解析】
连接OE,利用切线长定理得到AD=ED,CE=CB,且OD、OC分别为角平分线,利用平角的定义及等式性质得到∠COD为直角,进而确定出三角形ODE与三角形COD相似,由相似得比例列出关系式,可求OA的长,根据CD=DE+EC,等量代换得到AD+BC=CD,由梯形的面积公式可得S梯形ABCD=![]() AB(AD+BC)=
AB(AD+BC)=![]() ABCD,即可得到正确的选项;
ABCD,即可得到正确的选项;
解:∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,DA=DE=2,CE=CB=4,
∴AD∥BC,
∴CD=DE+EC=AD+BC,选项①正确;
在Rt△ADO和Rt△EDO中,
![]() ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,即∠DOC=90°,选项②正确;
∴∠DOC=∠DEO=90°,又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴![]() ,即OE2=DEEC=8,
,即OE2=DEEC=8,
∴OE=![]() ,
,
∴OA=OE=![]() ,选项④错误;
,选项④错误;
而S梯形ABCD=![]() AB(AD+BC)=
AB(AD+BC)=![]() ABCD,选项③错误;
ABCD,选项③错误;
则正确的选项有①②.
故答案为:①②.

【题目】已知二次函数y=ax2﹣bx+c的y与x的部分对立值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论①抛物线的开口向下:②其图象的对称轴为x=1:③当x<1时.函数值y随x的增大而增大,④方程ax2+bx+c=0有一个根大于4.其中正确的结论有_____