Question

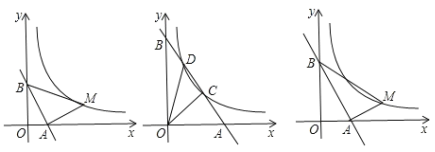
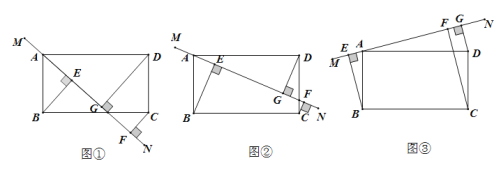
【题目】在矩形ABCD中，直线MN经过点A，BE⊥MN于点E，CF⊥MN于点F，DG⊥MN于点G.

(1)当MN绕点A旋转到图①位置时，求证:BE +CF =DG; .

(2)当MN绕点A旋转到图②和图③位置时，线段BE，CF，DG之间又有怎样的数量关系?

请写出你的猜想，不需要证明;

(3)在(1)(2)的条件下，若CD =2AE =6，EF =43，则CF= 。

Answer 1

【答案】(1)证明见解析；(2)或.

【解析】

（1）过点C作CH⊥DG于点H，证和四边形HGFC为矩形即可得出答案；

（2）图②过点C作CH⊥BE于点H，可知四边形FCGE为矩形，△BCH≌△DMG即可得出答案，图③过点D作DH⊥CF于点H，可知四边形FCDH为矩形，△ABE≌△DCH，即可得出答案.

解：(1)证明:过点C作CH⊥DG于点H，则∠DHC＝∠AEB=90°.

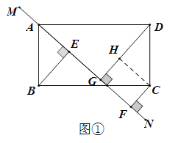
∵∠ABE+∠BAE=90°，∠BAE+∠DAG=90°

∴∠ABE=∠DAG

∵∠DAG+∠ADG=90°，∠ADG+∠CDH=90°，

∴∠DAG=∠CDH

∴∠ABE=∠CDH

在△ABE与△CDH中，∠ABE=∠CDH，∠BEA=∠CHD=90°,AB=DC

∴△ABE≌△CDH

∴BE=DH

∴四边形HGFC为矩形

(2)图②：

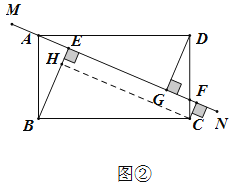
理由：过点C作CH⊥BE于点H，与（1）同理四边形FCGE为矩形，CF=EH，

∴CH∥MN，∠BHC=90°

∴∠HBC+∠HCB=90°

又∵∠HBC+∠ABE=90°

∴∠ABE=∠HCB

∵∠BAE+∠DMG=90°，∠BAE+∠ABE=90°

∴∠DMG=∠ABE=∠HCB

在△BCH与△DMG中，∠BHC=∠DGM=90°，∠HCB=∠DMG，BC=DM

∴△BCH≌△DMG

∴BH=DG

∴

图③：

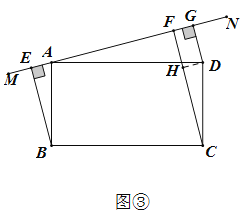
理由：过点D作DH⊥CF于点H，与（1）同理四边形FCDH为矩形，DG=FH，

∵∠CDH+∠ADH=90°，∠ADH+∠GDA=90°

∴∠CDH=∠GDA

∵∠GAD+∠GDA=90°，∠GAD+∠EAB=90°

∴∠GDA=∠EAB

∴∠EAB=∠CDH

在△ABE与△DCH中，∠BEA=∠CHD=90°，∠EAB=∠CDH，AB=DC

∴△ABE≌△DCH

∴BE=CH

∴CF-CH=CF-BE=FH=DG

（3）略