Question

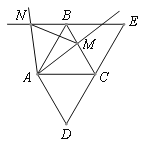
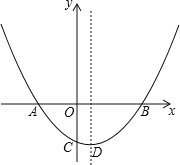
【题目】如图，抛物线y=ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，与y轴交于点C．

（1）求抛物线的解析式及顶点D的坐标；

（2）点P在抛物线的对称轴上，当△ACP的周长最小时，求出点P的坐标；

（3）若点M为抛物线第四象限内一点，连接BC、CM、BM，求当△BCM的面积最大时点M的坐标.

Answer 1

【答案】（1）抛物线解析式为y=（x﹣）2﹣，抛物线的顶点坐标为（，﹣），（3）点M的坐标为（1，－1）.

【解析】试题分析：（1）利用待定系数法求出抛物线解析式；

（2）确定出当△ACP的周长最小时，点P就是BC和对称轴的交点，利用两点间的距离公式计算即可．

（3）作出辅助线，利用tan∠MDN=2或，建立关于点N的横坐标的方程，求出即可．

试题解析：（1）∵抛物线y=ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，

∴

∴，

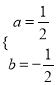∴抛物线解析式为y=x2﹣x﹣1=（x﹣）2﹣，

∴抛物线的顶点坐标为（，﹣），

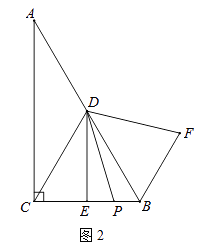
（2）如图1，

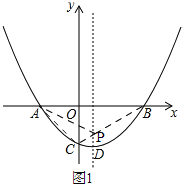
连接BC与抛物线对称轴的交点就是点P，连接AC，AP，

∵点A，B关于抛物线对称轴对称，

∴PA=PB，

∵B（2，0），C（0，﹣1），

∴直线BC解析式为y=x﹣1，

∵点P在抛物线对称轴上，

∴点P的横坐标为，

∴点P的纵坐标为﹣，

∴P（，﹣），

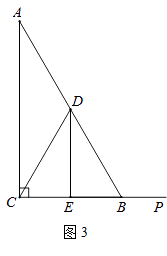
（3）设M（x， ），过点M作x轴的垂线交BC于点N，则点N（x， ）

∴==

故当x=1时，S△BMC面积最大，此时，

所以当△BCM的面积最大时点M的坐标为（1，－1）.