题目内容
【题目】问题提出
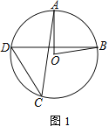
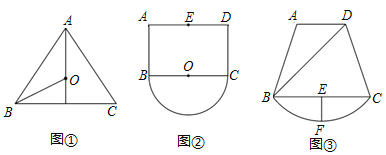
(1)如图①,在△ABC中,AB=AC=10,BC=12,点O是△ABC的外接圆的圆心,则OB的长为
问题探究
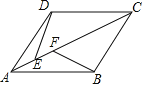
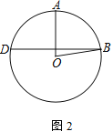
(2)如图②,已知矩形ABCD,AB=4,AD=6,点E为AD的中点,以BC为直径作半圆O,点P为半圆O上一动点,求E、P之间的最大距离;
问题解决
(3)某地有一块如图③所示的果园,果园是由四边形ABCD和弦CB与其所对的劣弧场地组成的,果园主人现要从入口D到![]() 上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120
上的一点P修建一条笔直的小路DP.已知AD∥BC,∠ADB=45°,BD=120![]() 米,BC=160米,过弦BC的中点E作EF⊥BC交
米,BC=160米,过弦BC的中点E作EF⊥BC交![]() 于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
于点F,又测得EF=40米.修建小路平均每米需要40元(小路宽度不计),不考虑其他因素,请你根据以上信息,帮助果园主人计算修建这条小路最多要花费多少元?
【答案】(1)![]() ;(2)E、P之间的最大距离为7;(3)修建这条小路最多要花费
;(2)E、P之间的最大距离为7;(3)修建这条小路最多要花费![]() 元.
元.
【解析】
(1)若AO交BC于K,则AK=8,在Rt△BOK中,设OB=x,可得x2=62+(8﹣x)2,解方程可得OB的长;
(2)延长EO交半圆于点P,可求出此时E、P之间的最大距离为OE+OP的长即可;
(3)先求出![]() 所在圆的半径,过点D作DG⊥BC,垂足为G,连接DO并延长交
所在圆的半径,过点D作DG⊥BC,垂足为G,连接DO并延长交![]() 于点P,则DP为入口D到
于点P,则DP为入口D到![]() 上一点P的最大距离,求出DP长即可求出修建这条小路花费的最多费用.
上一点P的最大距离,求出DP长即可求出修建这条小路花费的最多费用.
(1)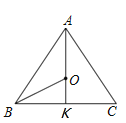
如图,若AO交BC于K,
∵点O是△ABC的外接圆的圆心,AB=AC,
∴AK⊥BC,BK=![]() ,
,
∴AK=![]() ,
,
在Rt△BOK中,OB2=BK2+OK2,设OB=x,
∴x2=62+(8x)2,
解得x=![]() ,
,
∴OB=![]() ;
;
故答案为:![]() .
.
(2)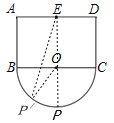
如图,连接EO,延长EO交半圆于点P,可求出此时E、P之间的距离最大,
∵在![]() 是任意取一点异于点P的P′,连接OP′,P′E,
是任意取一点异于点P的P′,连接OP′,P′E,
∴EP=EO+OP=EO+OP′>EP′,即EP>EP′,
∵AB=4,AD=6,
∴EO=4,OP=OC=![]() ,
,
∴EP=OE+OP=7,
∴E、P之间的最大距离为7.
(3)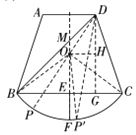
作射线FE交BD于点M,
∵BE=CE,EF⊥BC,![]() 是劣弧,
是劣弧,
∴![]() 所在圆的圆心在射线FE上,
所在圆的圆心在射线FE上,
假设圆心为O,半径为r,连接OC,则OC=r,OE=r40,BE=CE=![]() ,
,
在Rt△OEC中,r2=802+(r40)2,
解得:r=100,
∴OE=OFEF=60,
过点D作DG⊥BC,垂足为G,
∵AD∥BC,∠ADB=45°,
∴∠DBC=45°,
在Rt△BDG中,DG=BG=![]() ,
,
在Rt△BEM中,ME=BE=80,
∴ME>OE,
∴点O在△BDC内部,
∴连接DO并延长交![]() 于点P,则DP为入口D到
于点P,则DP为入口D到![]() 上一点P的最大距离,
上一点P的最大距离,
∵在![]() 上任取一点异于点P的点P′,连接OP′,P′D,
上任取一点异于点P的点P′,连接OP′,P′D,
∴DP=OD+OP=OD+OP′>DP′,即DP>DP′,
过点O作OH⊥DG,垂足为H,则OH=EG=40,DH=DGHG=DGOE=60,
∴![]() ,
,
∴DP=OD+r=![]() ,
,
∴修建这条小路最多要花费40×![]() 元.
元.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】2018年某省实施人才引进政策,对引进人才给予资金扶持和落户优惠,海内外英才纷纷向组织部门递交报名表.为了了解报名人员年龄结构情况,抽样调查了50名报名人员的年龄(单位:岁),将抽样得到的数据分成5组,统计如下表:
分组 | 频数(人数) | 频率 |
30岁以下 | 0.16 | |
大于30岁不大于40岁 | 20 | 0.40 |
大于40岁不大于50岁 | 14 | |
大于50岁不大于60岁 | 6 | 0.12 |
60岁以上 |
(1)请将表格中空格填写完整;
(2)样本数据的中位数落在_____,若把样本数据制成扇形统计图,则“大于30岁不大于40岁”的圆心角为______度;
(3)如果共有2000人报名,请你根据上面数据,估计年龄不大于40岁的报名人员会有多少人?
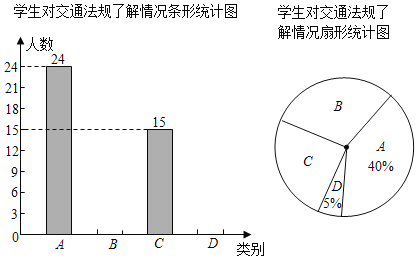
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
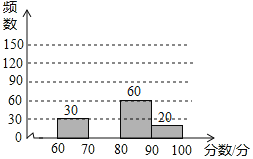
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?