题目内容
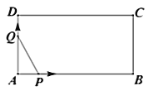
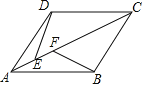
【题目】如图,菱形ABCD的边长为3,∠BAD=60°,点E、F在对角线AC上(点E在点F的左侧),且EF=1,则DE+BF最小值为_____
【答案】![]()
【解析】
作DM∥AC,使得DM=EF=1,连接BM交AC于F,先证明四边形DEFM是平行四边形,由此得出DE=FM,推出DE+BF=FM+FB=BM,根据两点之间线段最短可知,此时DE+FB最短,由四边形ABCD是菱形,在Rt△BDM中,根据BM=![]() 计算即可.
计算即可.
如图,作DM∥AC,使得DM=EF=1,连接BM交AC于F,

∵DM=EF,DM∥EF,
∴四边形DEFM是平行四边形,
∴DE=FM,
∴DE+BF=FM+FB=BM,
根据两点之间线段最短可知,此时DE+FB最短,
∵四边形ABCD是菱形,AB=3,∠BAD=60°
∴AD=AB,
∴△ABD是等边三角形,
∴BD=AB=3,
在Rt△BDM中,BM=![]() =
=![]()
∴DE+BF的最小值为![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目