ƒøƒ⁄»ð
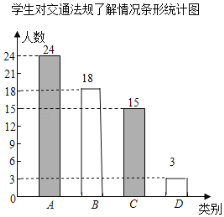
°æƒø°ø°∞ª˙∂Ø≥µ–– ªµΩ∞þ¬Ìœþ“™¿Ò»√––»À°±µ»ΩªÕ®∑®πÊ µ ©∫Û£¨ƒ≥–£π≤”–3000»À£¨ ˝—ßøŒÕ‚ µº˘–°◊ÈæÕ∂‘’‚–©ΩªÕ®∑®πʵƒ¡ÀΩ‚«Èøˆ‘⁄»´–£Àʪ˙µ˜≤È¡À≤ø∑÷—ß…˙£¨µ˜≤ÈΩ·π˚∑÷Œ™Àƒ÷÷£∫A£Æ∑«≥£¡ÀΩ‚£¨B£Æ±»Ωœ¡ÀΩ‚£¨C£Æª˘±æ¡ÀΩ‚£¨D£Æ≤ªÃ´¡ÀΩ‚£¨ µº˘–°◊È∞—¥À¥Œµ˜≤ÈΩ·π˚’˚¿Ì≤¢ªÊ÷∆≥…œ¬√Ê≤ªÕÍ’˚µƒÃı–ŒÕ≥º∆Õº∫Õ…»–ŒÕ≥º∆Õº£Æ
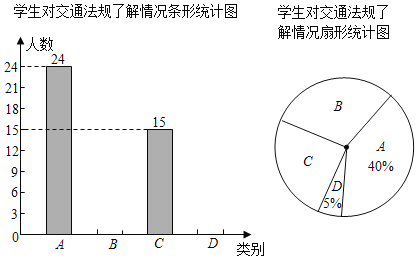
«ÎΩ·∫œÕº÷–À˘∏¯µƒ–≈œ¢Ω‚¥œ¬¡–Œ £∫
£®1£©…»–ŒÕ≥º∆Õº÷–CÀ˘∂‘”¶µƒ…»–Œ‘≤–ƒΩ«∂» ˝Œ™°° °°£ªπ¿º∆»´–£∑«≥£¡ÀΩ‚ΩªÕ®∑®πʵƒ”–°° °°»À£Æ
£®2£©≤π»´Ãı–ŒÕ≥º∆Õº£ª
£®3£©—ß–£◊º±∏¥”◊ȃ⁄µƒº◊°¢““°¢±˚°¢∂°ÀƒŒª—ß…˙÷–Àʪ˙≥È»°¡Ω√˚—ß…˙≤Œº” –«¯ΩªÕ®∑®πÊæ∫»¸£¨«Î”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®«Û±˚∫Õ∂°¡Ω√˚Õ¨—ßÕ¨ ¬±ª—°÷–µƒ∏≈¬ £Æ
°æ¥∞∏°ø£®1£©90°„£¨1200£ª£®2£©œÍº˚Ω‚Œˆ£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©”…Aµƒ»À ˝º∞∆‰À˘’º∞Ÿ∑÷±»ø…µ√◊лÀ ˝£¨”√360°„≥À“‘C»À ˝À˘’º±»¿˝£¨”…◊лÀ ˝ø…«Û»´–£∑«≥£¡ÀΩ‚ΩªÕ®∑®πʵƒ»À ˝º¥ø…µ√£ª
£®2£©◊лÀ ˝≥À“‘Dµƒ∞Ÿ∑÷±»«Ûµ√∆‰»À ˝£¨‘Ÿ∏˘æð∏˜¿ý–Õ»À ˝÷Æ∫Õµ»”⁄◊лÀ ˝«Ûµ√Bµƒ»À ˝£¨æð¥À≤π»´Õº–Œº¥ø…µ√£ª
£®3£©ª≠ ˜◊¥Õº¡–≥ˆÀ˘”–µ»ø…ƒÐΩ·π˚£¨‘Ÿ¿˚”√∏≈¬ π´ Ωº∆À„ø…µ√£Æ
Ω‚£∫£®1£©±æ¥Œµ˜≤ȵƒ—ß…˙◊лÀ ˝Œ™24°¬40%£Ω60£®»À£©£¨
°ý…»–ŒÕ≥º∆Õº÷–CÀ˘∂‘”¶…»–Œµƒ‘≤–ƒΩ«∂» ˝ «360°„°¡![]() £Ω90°„£¨
£Ω90°„£¨
»´–£∑«≥£¡ÀΩ‚ΩªÕ®∑®πʵƒ”–£∫3000°¡40%£Ω1200£®»À£©£¨
π ¥∞∏Œ™£∫90°„£¨1200£ª
£®2£©D¿ý±»À ˝Œ™60°¡5%£Ω3£¨
‘ÚB¿ý±»À ˝Œ™60©Å£®24+15+3£©£Ω18£¨
≤π»´Ãı–ŒÕº»Áœ¬£∫
£®3£©ª≠ ˜◊¥ÕºŒ™£∫
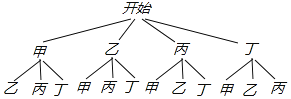
π≤”–12÷÷µ»ø…ƒÐµƒΩ·π˚ ˝£¨∆‰÷–±˚∫Õ∂°¡Ω√˚—ß…˙Õ¨ ±±ª—°÷–µƒΩ·π˚ ˝Œ™2£¨
À˘“‘±˚∫Õ∂°¡Ω√˚—ß…˙Õ¨ ±±ª—°÷–µƒ∏≈¬ Œ™![]() £Ω
£Ω![]() £Æ
£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏