题目内容
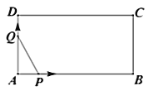
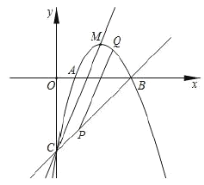
【题目】如图,已知![]() 的半径为1,
的半径为1,![]() 是
是![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线
的切线![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 交
交![]() 于
于![]() 点,四边形
点,四边形![]() 是平行四边形.
是平行四边形.

(1)求![]() 的长:
的长:
(2)![]() 是
是![]() 的切线吗?若是,给出证明;若不是,说明理由.
的切线吗?若是,给出证明;若不是,说明理由.
【答案】(1)2;(2)是,理由见解析
【解析】
(1)连接BD,由DE是![]() 的直径,利用直径所对的圆周角为直角可知:∠DBE=90°,由平行四边形的性质可知:BC∥OE,BC=OE=1,在Rt△ABD中,利用直角三角形斜边中线定理可得AD的长;
的直径,利用直径所对的圆周角为直角可知:∠DBE=90°,由平行四边形的性质可知:BC∥OE,BC=OE=1,在Rt△ABD中,利用直角三角形斜边中线定理可得AD的长;
(2)连接OB,由BC∥OD,BC=OD,可得四边形BCDO是平行四边形,根据切线的性质可知:OD⊥AD,进而得到四边形BCDO是矩形,由矩形的性质可知OB⊥CB,继而求证BC为圆![]() 的切线.
的切线.
(1)如图,连接![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
, ![]() ,
,
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
(2)是,理由如下:
如图,连接![]() .
.
∵![]() ,
, ![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∵![]() 为圆
为圆![]() 的切线,
的切线,
∴![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
∴则![]() 为圆
为圆![]() 的切线.
的切线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目