题目内容
【题目】为了庆祝“五四”青年节,我市某中学举行了书法比赛,赛后随机抽查部分参赛同学成绩(满分为100分),并制作成图表如下
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
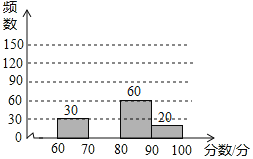
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩不低于80分的学生有多少人?
【答案】(1)200;90,0.3;(2)补图见解析;(3)54°;(4)240人
【解析】
(1)根据60≤x<70的频数及其频率求得总人数,进而计算可得m、n的值;
(2)根据(1)的结果,可以补全直方图;
(3)用360°乘以样本中分数段60≤x<70的频率即可得;
(4)总人数乘以样本中成绩80≤x<100范围内的学生人数所占比例.
解:(1)本次调查的总人数为30÷0.15=200人,
则m=200×0.45=90,n=60÷200=0.3,
故答案为200、90、0.3;
(2)补全频数分布直方图如下:
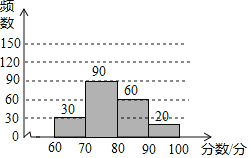
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是360°×0.15=54°,
故答案为54°;
(4)600×![]() =240,
=240,
答:估计该校成绩不低于80分的学生有240人.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目