Question

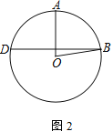
【题目】如图，在⊙O中，半径OA与弦BD垂直，点C在⊙O上，∠AOB＝80°

(1) 若点C在优弧BD上，求∠ACD的大小

(2) 若点C在劣弧BD上，直接写出∠ACD的大小

Answer 1

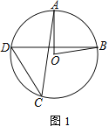
【答案】（1）∠ACD=40°；（2）∠ACD=40°或140°．

【解析】

（1）由AO⊥BD，根据垂径定理可得，再利用等弧对等角，以及圆周角定理即可求出结果；

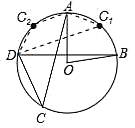
（2）如图所示，点C有两个位置，分别利用圆周角定理的推论和圆周角定理求出即可.

解：（1）∵AO⊥BD，

∴，

∴∠AOB=2∠ACD，

∵∠AOB=80°，

∴∠ACD=40°；

（2）如图，①当点C1在上时，∠AC1D=∠ACD=40°；

②当点C2在上时，∵∠AC2D+∠ACD=180°，∴∠AC2D=140°.

综上所述，∠ACD=40°或140°．