ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy=![]() x2+bx+c¾¹ż”÷ABCµÄČżøö¶„µć£¬ĘäÖŠµćA£Ø0£¬1£©£¬µćB£Ø©9£¬10£©£¬AC”ĪxÖį£¬µćPŹ±Ö±ĻßACĻĀ·½Å×ĪļĻßÉĻµÄ¶Æµć£®
x2+bx+c¾¹ż”÷ABCµÄČżøö¶„µć£¬ĘäÖŠµćA£Ø0£¬1£©£¬µćB£Ø©9£¬10£©£¬AC”ĪxÖį£¬µćPŹ±Ö±ĻßACĻĀ·½Å×ĪļĻßÉĻµÄ¶Æµć£®

£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»£Ø2£©¹żµćPĒŅÓėyÖįĘ½ŠŠµÄÖ±ĻßlÓėÖ±ĻßAB”¢AC·Ö±š½»ÓŚµćE”¢F£¬µ±ĖıߊĪAECPµÄĆ껿×ī“óŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©µ±µćPĪŖÅ×ĪļĻߵĶ„µćŹ±£¬ŌŚÖ±ĻßACÉĻŹĒ·ń“ęŌŚµćQ£¬Ź¹µĆŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬Čō“ęŌŚ£¬Ēó³öµćQµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y=![]() x2+2x+1£»£Ø2£©P£Ø©
x2+2x+1£»£Ø2£©P£Ø©![]() £¬©
£¬©![]() £©£»£Ø3£©£Ø©4£¬1£©»ņ£Ø3£¬1£©£®
£©£»£Ø3£©£Ø©4£¬1£©»ņ£Ø3£¬1£©£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓĆ“ż¶ØĻµŹż·ØĒó³öÅ×ĪļĻß½āĪöŹ½¼“æÉ£»£Ø2£©ÉčµćP£Øm£¬![]() m2+2m+1£©£¬±ķŹ¾³öPE=©
m2+2m+1£©£¬±ķŹ¾³öPE=©![]() m2©3m£¬ŌŁÓĆSĖıߊĪAECP=S”÷AEC+S”÷APC=
m2©3m£¬ŌŁÓĆSĖıߊĪAECP=S”÷AEC+S”÷APC=![]() AC”ĮPE£¬½ØĮ¢ŗÆŹż¹ŲĻµŹ½£¬Ēó³ö¼«Öµ¼“æÉ£»£Ø3£©ĻČÅŠ¶Ļ³öPF=CF£¬ŌŁµĆµ½”ĻPCF=”ĻEAF£¬ŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬·ÖĮ½ÖÖĒéæö¼ĘĖć¼“æÉ£®
AC”ĮPE£¬½ØĮ¢ŗÆŹż¹ŲĻµŹ½£¬Ēó³ö¼«Öµ¼“æÉ£»£Ø3£©ĻČÅŠ¶Ļ³öPF=CF£¬ŌŁµĆµ½”ĻPCF=”ĻEAF£¬ŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬·ÖĮ½ÖÖĒéæö¼ĘĖć¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©”ßµćA£Ø0£¬1£©£®B£Ø©9£¬10£©ŌŚÅ×ĪļĻßÉĻ£¬
”ą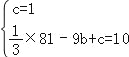 £¬
£¬
”ąb=2£¬c=1£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=![]() x2+2x+1£¬
x2+2x+1£¬
£Ø2£©”ßAC”ĪxÖį£¬A£Ø0£¬1£©
”ą![]() x2+2x+1=1£¬
x2+2x+1=1£¬
”ąx1=6£¬x2=0£¬
”ąµćCµÄ×ų±ź£Ø©6£¬1£©£¬
”ßµćA£Ø0£¬1£©£®B£Ø©9£¬10£©£¬
”ąÖ±ĻßABµÄ½āĪöŹ½ĪŖy=©x+1£¬
ÉčµćP£Øm£¬![]() m2+2m+1£©
m2+2m+1£©
”ąE£Øm£¬©m+1£©
”ąPE=©m+1©£Ø![]() m2+2m+1£©=©
m2+2m+1£©=©![]() m2©3m£¬
m2©3m£¬
”ßAC”ĶEP£¬AC=6£¬
”ąSĖıߊĪAECP
=S”÷AEC+S”÷APC
=![]() AC”ĮEF+
AC”ĮEF+![]() AC”ĮPF
AC”ĮPF
=![]() AC”Į£ØEF+PF£©
AC”Į£ØEF+PF£©
=![]() AC”ĮPE
AC”ĮPE
=![]() ”Į6”Į£Ø©
”Į6”Į£Ø©![]() m2©3m£©
m2©3m£©
=©m2©9m
=©£Øm+![]() £©2+
£©2+![]() £¬
£¬
”ß©6£¼m£¼0
”ąµ±m=©![]() Ź±£¬ĖıߊĪAECPµÄĆ껿µÄ×ī“óÖµŹĒ
Ź±£¬ĖıߊĪAECPµÄĆ껿µÄ×ī“óÖµŹĒ![]() £¬
£¬
“ĖŹ±µćP£Ø©![]() £¬©
£¬©![]() £©£®
£©£®
£Ø3£©”ßy=![]() x2+2x+1=
x2+2x+1=![]() £Øx+3£©2©2£¬
£Øx+3£©2©2£¬
”ąP£Ø©3£¬©2£©£¬
”ąPF=yF©yP=3£¬CF=xF©xC=3£¬
”ąPF=CF£¬
”ą”ĻPCF=45”ć
Ķ¬ĄķæÉµĆ£ŗ”ĻEAF=45”ć£¬
”ą”ĻPCF=”ĻEAF£¬
”ąŌŚÖ±ĻßACÉĻ“ęŌŚĀś×ćĢõ¼žµÄQ£¬
ÉčQ£Øt£¬1£©ĒŅAB=9![]() £¬AC=6£¬CP=3
£¬AC=6£¬CP=3![]()
”ßŅŌC”¢P”¢QĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬
¢Łµ±”÷CPQ”×”÷ABCŹ±£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąt=©4£¬
”ąQ£Ø©4£¬1£©
¢Śµ±”÷CQP”×”÷ABCŹ±£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąt=3£¬
”ąQ£Ø3£¬1£©£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø”¾ĢāÄæ”æ³õ¶žÄ³°ą12ĆūĶ¬Ń§Į·Ļ°¶ØµćĶ¶Ąŗ£¬ĆæČĖø÷Ķ¶10“Ī£¬½ųĒņŹżĶ³¼ĘČē±ķ£®Õā12ĆūĶ¬Ń§½ųĒņŹżµÄÖŚŹżŹĒ£Ø””””£©
½ųĒņŹż£Øøö£© | 1 | 2 | 3 | 4 | 5 | 7 |
ČĖŹż£ØČĖ£© | 1 | 1 | 4 | 2 | 3 | 1 |
A. 3.75B. 3C. 3.5D. 7