��Ŀ����
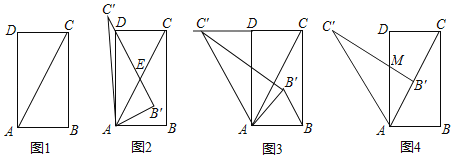
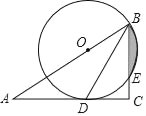
����Ŀ������ѧ��У�С�����ֽ����鲻ͬ�ĵ���ֱ�����ǰ������ת���ܵõ�һ����ۣ�������һ�����ǰ�Rt��ABC��AB��BC��4����BΪֱ�ǣ�����һ�����ֱ�����ǰ��ֱ�Ƕ������б��AC���е�O���������ǰ��Ƶ�O��ת�����ǰ����ֱ�DZ߷ֱ�AB��BC�����ӳ�����E��F���㣬��ͼ����������ת���ǰ�����ͼ�ε����������
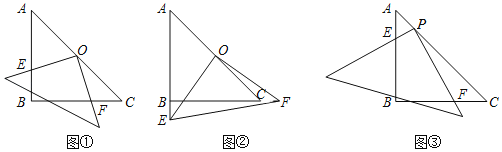
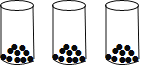
��1�����ǰ��Ƶ�O��ת����OFC�Ƿ��ܳ�Ϊ����ֱ�������Σ����ܣ����CF�������ܣ���˵�����ɣ�
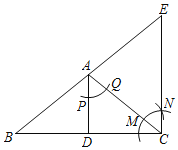
��2�����ǰ��Ƶ�O��ת���߶�OE��OF֮����ʲô������ϵ����ͼ������֤����
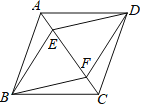
��3���������ǰ��ֱ��ԭ�����б���ϵĵ�P������ͼ��������![]() ��PF��PE��������������ϵ��֤���㷢�ֵĽ��ۣ�
��PF��PE��������������ϵ��֤���㷢�ֵĽ��ۣ�
���𰸡���1��CF��2��CF��4����2��OE��OF�����������������3��PF��4PE�������������.
��������
��OFC�ܳ�Ϊ����ֱ�������Σ�����OFC��90������COF��90�����������FC�ij����ɣ���2��OE��OF������OB��CF��������֪������֤OB��OC����EBO=��OCF=135�㡢��EOB����FOC������ASA֤����OEB�ա�OFC�����ɵ�OE=OF����3��PF��4PE����ͼ��������P��PM��AB��M��PN��BC��N��֤����PME�ס�PNF����APM�ס�PCN���������������ε����ʿɵ�![]() ���ɴ˼������
���ɴ˼������![]() �����۵�֤.
�����۵�֤.
�⣺��1����OFC�ܳ�Ϊ����ֱ�������Σ�
��Rt��ABC��AB��BC��4��
���C��45�㣬
�ߡ�OFC�ǵ���ֱ�������Σ�
���OFC��90����COF��90�㣬
����OFC��90��ʱ��OF��BC��
�ߡ�B��90�㣬
��OF��AB��
�ߵ�O��AC���е㣬
���F��BC���е㣬
��CF��![]() BC��2��
BC��2��
����COF��90��ʱ����ʱ��F�͵�B�غϣ�CF��BC��4��
����CF��2��CF��4��
��2��OE��OF��
���ɣ�����OB��CF����ͼ����
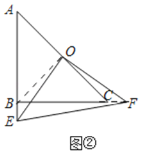
��AB��BC����ABC��90�㣬O��ΪAC���е㣬
��OB��![]() AC��OC����BOC��90������ABO=��ACB=45�㣬
AC��OC����BOC��90������ABO=��ACB=45�㣬
���EBO=��OCF=135�㣮
�ߡ�EOF��90�㣬
���EOB����FOC��
�ڡ�OEB�͡�OFC�У�
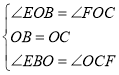 ��
��
���OEB�ա�OFC��
��OE=OF��
��3��PF��4PE����ͼ��������P��PN��AB��N��PM��BC��M��
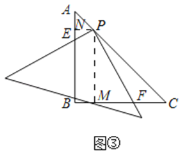
�ߡ�B��90�㣬
���MPN��90�㣬
�ߡ�EPF��90�㣬
���EPN����FPM��
�ߡ�ENP����FMP��90�㣬
���PNE�ס�PMF��
��![]() ��
��
�ߡ�APN�͡�PCMΪ����ֱ�������Σ�
���APM�ס�PCN��
��![]() ,
,
��![]()
��![]() ��
��
��![]() ��
��
��![]() ��
��
����PF��4PE��