题目内容
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).
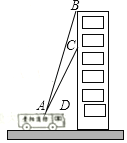
【答案】第二次施救时云梯与水平线的夹角∠BAD约为71°.
【解析】试题分析:延长AD交BC所在直线于点E.解Rt△ACE,得出CE=AEtan60°=15![]() 米,解Rt△ABE,由tan∠BAE=
米,解Rt△ABE,由tan∠BAE=![]() ,得出∠BAE≈71°.
,得出∠BAE≈71°.
试题解析:延长AD交BC所在直线于点E,
由题意,得BC=17米,AE=15米,∠CAE=60°,∠AEB=90°,
在Rt△ACE中,tan∠CAE=![]() ,
,
∴CE=AEtan60°=15![]() 米,
米,
在Rt△ABE中,tan∠BAE=![]() ,
,
∴∠BAE≈71°,
答:第二次施救时云梯与水平线的夹角∠BAD约为71°.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目