题目内容
【题目】综合与实践
一、问题情境
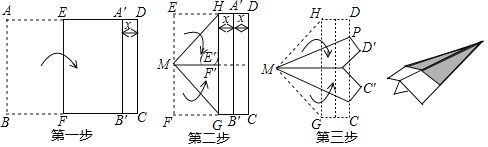
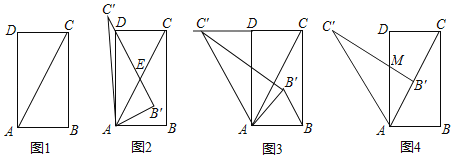
在综合与实践课上,老师组织同学们以“直角三角形的旋转”为主题开展数学活动.如图1,矩形ABCD中,AD=2AB,连接AC,将△ABC绕点A旋转到某一位置,观察图形,提出问题并加以解决.
二、实践操作,解决问题
(1)如图2,慎思组的间学将图1中的△ABC以点A为旋转中心,按逆时针方向旋转,得到△A'B'C',此时B'C'过点D,则∠ADB′=____度.
(2)博学组的同学在图2的基础上继续旋转到图3,此时点C落在CD的延长线上,连接BB',该组提出下面两个问题,并请你解决该组提出的这两个问题.
①C'D和AB有何数量关系?并说明理由.
②BB'和AC'有何位置关系?并说明理由.
(3)精英组的同学在图3的基础上按逆时针方向旋转至AB'与对角线AC重合时,B'C'与AD交于点M,如图4,则S![]() :S△ABC=_____.
:S△ABC=_____.
【答案】(1)30;(2)①C′D=AB;②AC′∥BB′;(3)3:4.
【解析】
(1)由旋转性质知AB=AB′、∠B′=∠B=90°,结合AD=BC=2AB可得AD=2AB′,根据直角三角形的性质可得答案;
(2)①利用“HL”证Rt△ADC′≌Rt△ABC即可得;②过点C′作C′H垂直于BA延长线于点H,证△C′HA≌△C′B′A得∠HAC′=∠C′AB,由AB=AB′知∠ABB′=∠AB′B,据此根据∠HAB′=∠ABB′+∠AB′B可得2∠C′AB′=2∠AB′B,即可得证;
(3)设AB=a,则BC=2a,求出MC′:B′C′的值即可解决问题.
解:(1)由题意知△ABC≌△AB′C′,
∴AB=AB′、∠B′=∠B=90°,
∵AD=BC=2AB,
∴在Rt△AB′D中,AD=2AB′,
则∠ADB′=30°,
故答案为:30;
(2)①C′D=AB,理由如下:
∵四边形ABCD是矩形,
∴AD=BC、∠ABC=∠ADC=∠ADC′=90°,
由旋转知AC′=AC,
在Rt△ADC′和Rt△ABC中,
∵![]() ,
,
∴Rt△ADC′≌Rt△ABC(HL),
∴C′D=AB;
②结论:AC′∥BB′;
理由:如图a,过点C′作C′H垂直于BA延长线于点H,

则四边形HADC′是矩形,
∴C′H=AD、AH=C′D=AB,
在△C′HA和△C′B′A中,
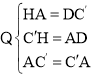
∴△C′HA≌△C′B′A(SSS),
∴∠HAC′=∠C′AB,
又∵AB=AB′,
∴∠ABB′=∠AB′B,
在△ABB′中,∠HAB′=∠ABB′+∠AB′B,即∠HAC′+∠C′AB′=∠ABB′+∠AB′B,
∴2∠C′AB′=2∠AB′B,
∴∠C′AB′=∠AB′B,
∴AC′∥BB′;
(3)如图4中,设AB=a,则BC=2a,
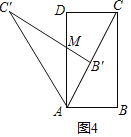
∵AD∥BC,
∴∠MAB′=∠ACB,
∵∠AB′M=∠B=90°,
∴△AB′M∽△CBA,
∴B′M:AB=AB′:BC,
∴B′M:a=a:2a,
∴BM′=![]()
∵B′C′=2a,
∴MC′=![]()
∴MC′:B′C′=3:4,
∴S△AC′M:S△ABC=3:4,
故答案为:3:4.

 阅读快车系列答案
阅读快车系列答案【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
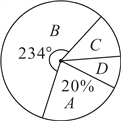
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.