Question

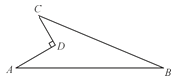
【题目】如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．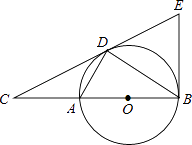

（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，BC=6， ．求BE的长．

Answer 1

【答案】
（1）证明：连结OD，

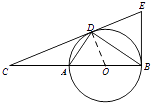
∵OB=OD，

∴∠OBD=∠BDO，

∵∠CDA=∠CBD，

∴∠CDA=∠ODB，

又∵AB是⊙O的直径，

∴∠ADB=90°，

∴∠ADO+∠ODB=90°，

∴∠ADO+∠CDA=90°，

即∠CDO=90°，

∴OD⊥CD，

∵OD是⊙O半径，

∴CD是⊙O的切线

（2）解：∵∠C=∠C，∠CDA=∠CBD

∴△CDA∽△CBD

∴

∵ ，BC=6，

∴CD=4，

∵CE，BE是⊙O的切线

∴BE=DE，BE⊥BC

∴BE2+BC2=EC2，即BE2+62=（4+BE）2

解得：BE= ．

【解析】（1） 由等边对等角及等量代换得∠CDA=∠ODB，由直径所对的圆周角是直角得∠ADO+∠ODB=90°，进而得∠ADO+∠CDA=90°，即∠CDO=90°，根据切线的判定即可得出结论；（2） 首先判断出△CDA∽△CBD，由相似三角形的性质得出CD=4，根据切线长定理得出BE=DE，BE⊥BC，最后根据勾股定理得出BE的长。