题目内容
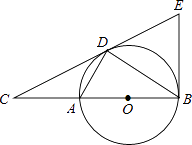
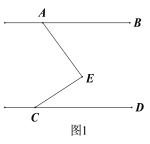
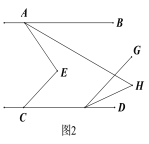
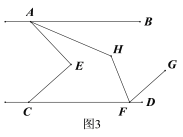
【题目】如图,△ABC和△CDE均为等边三角形,且点B,C,D在同一直线上,连结AD,BE,分别交CE和AC于点G,H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由;
(3)试猜想△CGH是什么特殊的三角形,并加以证明.

【答案】(1)证明见解析;(2)证明见解析;(3)△CGH是等边三角形.
【解析】
(1)证明△ACD≌△BCE即可得出答案;
(2)根据△ACD≌△BCE,
∴∠CBH=∠CAG,由∠ACB=∠ECD=60°,点B、C、D在同一条
直线上,得出∠ACB=∠ECD=∠ACG=60°
根据AC=BC即可证明;
(3)由△ACG≌△BCH,
∴CG=CH,根据∠ACG=60°即可证明.
解:(1)∵△ABC和△CDE均为等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴AD=BE
(2)∵△ACD≌△BCE,
∴∠CBH=∠CAG.
∵∠ACB=∠ECD=60°,点B,C,D在同一条直线上,
∴∠ACB=∠ECD=∠ACG=60°.
又∵AC=BC,
∴△BCH≌△ACG(ASA)
(3)△CGH是等边三角形,
理由:∵△ACG≌△BCH,
∴CG=CH,
又∵∠ACG=60°,
∴△CGH是等边三角形

练习册系列答案
相关题目
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?