题目内容
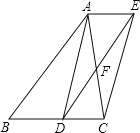
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.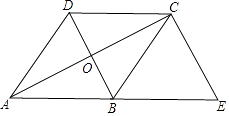
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4 ![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD是平行四边形
(2)解:∵四边形BECD是平行四边形,
∴DB∥CE,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠E=∠OBA,
∴AC⊥CE.
在直角△ACE中,∵∠E=60°,AC=4 ![]() ,
,
∴CE= ![]() =
= ![]() =4.
=4.
∵四边形BECD是平行四边形,
∴BD=CE=4,
∴S菱形ABCD= ![]() ACBD=
ACBD= ![]() ×4
×4 ![]() ×4=8
×4=8 ![]() .
.
【解析】(1)由菱形的性质得AB=CD,AB∥CD,又用等量代换得出BE=CD,BE∥CD,根据平行四边形的判定定理得出结论;(2)由平行四边形的性质得DB∥CE,由菱形的性质得AC⊥BD,进而 根据平行线的性质得出∠E=∠OBA,AC⊥CE.解直角三角形得CE的长度,最后根据平行四边形的性质及菱形面积公式得出结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?