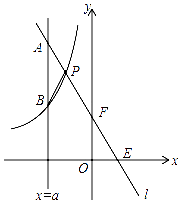Question

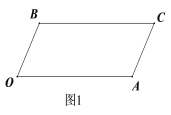
【题目】如图1所示，已知BC∥OA, ∠B=∠A=120°.

（1）证明：OB∥AC;

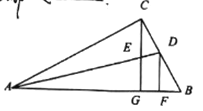
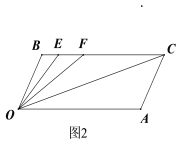
（2）如图2所示，若点E,F在BC上，且∠FOC=∠AOC,OE平分∠BOF，求∠EOC的度数.

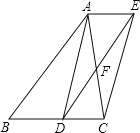
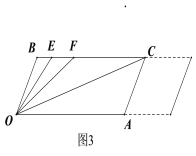
（3）在（2）的条件下，若左右平移AC，如图3所示，那么∠OCB∶∠OFB的比值是否随之发生变化？若变化，请说明理由；若不变化，请求出这个比值.

（4）在（2）和（3）的条件下，当∠OEB=∠OCA时，求∠OCA的度数.

Answer 1

【答案】(1) 答案见详解，(2) 答案见详解,(3) 答案见详解,(4) 答案见详解.

【解析】

（1）由同旁内角互补，两直线平行证明．

（2）由∠FOC=∠AOC，并且OE平分∠BOF得到∠EOC=∠EOF+∠FOC=（∠BOF+∠FOA）=∠BOA，算出结果．

（3）先得出结论：∠OCB：∠OFB的值不发生变化，理由为：由BC与AO平行，得到一对内错角相等，由∠FOC=∠AOC，等量代换得到一对角相等，再利用外角性质等量代换即可得证；

（4）设∠BOE=∠EOF=α，∠FOC=∠COA=β，根据外角的性质分别用α和β表示出∠OEB和∠OCA，由∠OEB=∠OCA，即可得出α=β=15°，求出∠OCA即可.

（1）∵BC∥OA，
∴∠B+∠O=180°，又∵∠B=∠A，
∴∠A+∠O=180°，
∴OB∥AC；
（2）∵∠B+∠BOA=180°，∠B=120°，
∴∠BOA=60°，
∵OE平分∠BOF，
∴∠BOE=∠EOF，又∵∠FOC=∠AOC，
∴∠EOC=∠EOF+∠FOC=（∠BOF+∠FOA）

=∠BOA=30°；
（3）结论：∠OCB：∠OFB的值不发生变化．理由为：
∵BC∥OA，
∴∠FCO=∠COA，
又∵∠FOC=∠AOC，
∴∠FOC=∠FCO，
∴∠OFB=∠FOC+∠FCO=2∠OCB，
∴∠OCB：∠OFB=1：2；
（4）由（1）知：OB∥AC，
则∠OCA=∠BOC，
由（2）可以设：∠BOE=∠EOF=α，∠FOC=∠COA=β，
则∠OCA=∠BOC=2α+β，
∠OEB=∠EOC+∠ECO=α+β+β=α+2β，
∵∠OEB=∠OCA，
∴2α+β=α+2β，
∴α=β，
∵∠AOB=60°，
∴α=β=15°，
∴∠OCA=2α+β=30°+15°=45°．