题目内容
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.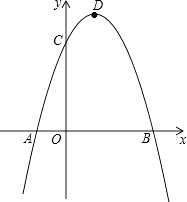
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),
∴根据题意,得 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)解:由y=﹣x2+2x+3=﹣(x﹣1)2+4得,D点坐标为(1,4),
∴CD= ![]() =
= ![]() ,
,
BC= ![]() =3
=3 ![]() ,
,
BD= ![]() =2
=2 ![]() ,
,
∵CD2+BC2=( ![]() )2+(3
)2+(3 ![]() )2=20,BD2=(2
)2=20,BD2=(2 ![]() )2=20,
)2=20,
∴CD2+BC2=BD2,
∴△BCD是直角三角形;
(3)解:存在.
y=﹣x2+2x+3对称轴为直线x=1.
①若以CD为底边,则P1D=P1C,
设P1点坐标为(x,y),根据勾股定理可得P1C2=x2+(3﹣y)2,P1D2=(x﹣1)2+(4﹣y)2,
因此x2+(3﹣y)2=(x﹣1)2+(4﹣y)2,
即y=4﹣x.
又P1点(x,y)在抛物线上,
∴4﹣x=﹣x2+2x+3,
即x2﹣3x+1=0,
解得x1= ![]() ,x2=
,x2= ![]() <1,应舍去,
<1,应舍去,
∴x= ![]() ,
,
∴y=4﹣x= ![]() ,
,
即点P1坐标为( ![]() ,
, ![]() ).
).
②若以CD为一腰,
∵点P2在对称轴右侧的抛物线上,由抛物线对称性知,点P2与点C关于直线x=1对称,
此时点P2坐标为(2,3).
∴符合条件的点P坐标为( ![]() ,
, ![]() )或(2,3).
)或(2,3).

【解析】(1)将A(﹣1,0)、B(3,0)代入二次函数y=ax2+bx﹣3a求得a、b的值即可确定二次函数的解析式;(2)分别求得线段BC、CD、BD的长,利用勾股定理的逆定理进行判定即可;(3)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.