题目内容
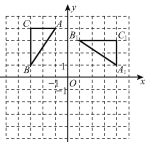
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
【答案】(1)(0,0);90;(2)画图见解析;平移距离为![]() .
.
【解析】
(1)利用旋转的性质可知,旋转中心在对应点连线的垂直平分线上,分别画AA1、BB1的垂直平分线,交点即为旋转中心;进而可得旋转角;(2)根据A2坐标可知,△ABC向右平移1个单位,向下平移5个单位,据此画出△A2B2C2即可,根据勾股定理求出AA1的长即可得平移距离.
(1)如图:分别连接AA1、BB1,作AA1、BB1的垂直平分线,交点为(0,0),
∴旋转中心为(0,0),∠AOA1为旋转角,
由图像可得∠AOA1=90°,
故答案为:(0,0);90;
(2)∵A(-1,4),A2(0,-1),
∴△ABC向右平移1个单位,向下平移5个单位,
∴△A2B2C2如图所示,
∴AA2=![]() =
=![]() .
.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目