题目内容
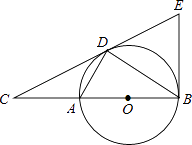
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
【答案】
(1)解:点A(﹣2,0)与点B关于x=1对称,得
B(4,0).
将A,B,C代入函数解析式,得
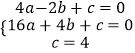 解得
解得 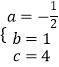 ,
,
抛物线的解析式为y=﹣ ![]() x2+x+4;
x2+x+4;
(2)解:不存在点F,使四边形ABFC的面积为15,理由如下:
如图1
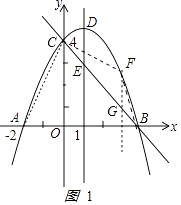 ,
,
AC的解析式为y=﹣x+4,
设F点坐标为(m,﹣ ![]() m2+m+4),G(m,﹣m+4),
m2+m+4),G(m,﹣m+4),
FG的长为(﹣ ![]() m2+m+4)﹣(﹣m+4)=﹣
m2+m+4)﹣(﹣m+4)=﹣ ![]() m2+2m,
m2+2m,
S四边形ABFC=S△ABC+S△ABF
= ![]() ABxC+
ABxC+ ![]() FG(xB﹣xA)
FG(xB﹣xA)
= ![]() ×6×4+
×6×4+ ![]() ×4(﹣
×4(﹣ ![]() m2+2m)=15,
m2+2m)=15,
化简,得
2m2﹣4m+3=0,
∵△=b2﹣4ac=16﹣4×2×3=﹣8<0,
方程无解,
∴P点不存在;
(3)解:当x=1时,﹣ ![]() x2+x+4=
x2+x+4= ![]() ,即D(1,
,即D(1, ![]() )
)
当x=1时,﹣x+4=3,即E(1,3),
DE= ![]() ﹣3=
﹣3= ![]() .
.
AC的解析式为y=﹣x+4,
设Q点坐标为(m,﹣ ![]() m2+m+4),P(m,﹣m+4),
m2+m+4),P(m,﹣m+4),
QP的长为|(﹣ ![]() m2+m+4)﹣(﹣m+4)|=|﹣
m2+m+4)﹣(﹣m+4)|=|﹣ ![]() m2+2m|.
m2+2m|.
由PQ∥DE,PQ=DE,得
|﹣ ![]() m2+2m|=
m2+2m|= ![]() .
.
﹣  m2+2m=
m2+2m= ![]() ,或)﹣
,或)﹣ ![]() m2+2m=﹣
m2+2m=﹣ ![]() ,
,
解得m1=1舍,m2=3,m3=2+ ![]() ,m4=2﹣
,m4=2﹣ ![]() .
.
P点坐标为(3,1)(2+ ![]() ,2﹣
,2﹣ ![]() )(2﹣
)(2﹣ ![]() ,2+
,2+ ![]() ).
).
【解析】(1)根据函数值相等的点关于对称轴对称,可得B点坐标,根据待定系数法,可得答案;(2)根据根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得FG的长,根据面积的和差,可得关于m的方程,根据解方程,可得答案;(3)根据平行四边形的对边相等,可得关于m的方程,根据解方程,可得答案.

【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.