题目内容
受不法投机商炒作的影响,去年黑豆价格出现了大幅度波动.1至3月份,黑豆价格大幅度上涨,其价格y1(万元/吨)与月份x(1≤x≤3,且x取整数)之间的关系如下表:
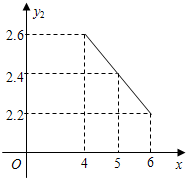
而从4月份起,黑豆价格大幅度走低,其价格y2(万元/吨)与月份x(4≤x≤6,且x取整数)之间的函数关系如图所示.
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出黑豆价格y1(万元/吨)与月份x之间所满足的函数关系式;观察如图,直接写出黑豆价格y2(万元/吨)与月份x之间所满足的一次函数关系式;
(2)某食品加工厂每月均在上旬进货,去年1至3月份的黑豆进货量p1(吨)与月份x之间所满足的函数关系式为p1=-10x+180(1≤x≤3,且x取整数);4至6月份黑豆进货量p2(吨)与月份x之间所满足的函数关系式为p2=30x-30(4≤x≤6,且x取整数).求在前6个月中该加工厂的黑豆进货金额最大的月份和该月的进货金额;
(3)去年7月份黑豆价格在6月的基础上下降了a%,进货量在6月份的基础上增加了2a%.使得7月份进货金额为363万元,请你计算出a的最大整数值.
(参考数据:
≈1.7,
≈2.2,
≈2.4,
≈2.6)
| 月份x | 1 | 2 | 3 |
| 价格y1(万元/吨) | 2.6 | 2.8 | 3 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出黑豆价格y1(万元/吨)与月份x之间所满足的函数关系式;观察如图,直接写出黑豆价格y2(万元/吨)与月份x之间所满足的一次函数关系式;
(2)某食品加工厂每月均在上旬进货,去年1至3月份的黑豆进货量p1(吨)与月份x之间所满足的函数关系式为p1=-10x+180(1≤x≤3,且x取整数);4至6月份黑豆进货量p2(吨)与月份x之间所满足的函数关系式为p2=30x-30(4≤x≤6,且x取整数).求在前6个月中该加工厂的黑豆进货金额最大的月份和该月的进货金额;
(3)去年7月份黑豆价格在6月的基础上下降了a%,进货量在6月份的基础上增加了2a%.使得7月份进货金额为363万元,请你计算出a的最大整数值.
(参考数据:
| 3 |
| 5 |
| 6 |
| 7 |

(1)利用表格可知y1与x是一次函数关系,设y1=kx+b,
由题意,得
,
解得
,
则y1=0.2x+2.4(1≤x≤3,且x取整数);
利用图象得可知y2与x是一次函数关系,设y2=ax+c,
由题意,得
,
解得
,
则y2=-0.2x+3.4(4≤x≤6,且x取整数);
(2)在前3个月中,设每月黑豆的进货金额为W1万元,
则W1=y1•p1=(0.2x+2.4)(-10x+180)=-2x2+12x+432=-2(x-3)2+450(1≤x≤3,且x取整数),
∴当x=3时,W1最大=450万元;
在4到6月份中,设每月黑豆的进货金额为W2万元,
则W2=y2•p2=(-0.2x+3.4)(30x-30)=-6x2+108x-102=-6(x-9)2+384(4≤x≤6,且x取整数),
∵9>6,而当4≤x≤6时,W2随x的增大而增大,
∴当x=6时,w2最大=330万元;
∵450>330,
∴在前6个月中,第3月份食品加工厂的黑豆进货金额最大,最大金额为450万元;
(3)6月份的黑豆价格为:y2=-0.2×6+3.4=2.2(万元/吨),
进货量为:p2=30×6-30=150(吨),
由题意,得2.2(1-a%)×150(1+2a%)=363,
整理,得a2-50a+500=0,
解得a=25±5
.
∵
≈2.2,
∴a≈14或a≈36.
∵所求为最大整数值,
∴a取36.
答:a的最大整数值为36.
由题意,得
|
解得
|
则y1=0.2x+2.4(1≤x≤3,且x取整数);
利用图象得可知y2与x是一次函数关系,设y2=ax+c,
由题意,得
|
解得
|
则y2=-0.2x+3.4(4≤x≤6,且x取整数);
(2)在前3个月中,设每月黑豆的进货金额为W1万元,
则W1=y1•p1=(0.2x+2.4)(-10x+180)=-2x2+12x+432=-2(x-3)2+450(1≤x≤3,且x取整数),
∴当x=3时,W1最大=450万元;
在4到6月份中,设每月黑豆的进货金额为W2万元,
则W2=y2•p2=(-0.2x+3.4)(30x-30)=-6x2+108x-102=-6(x-9)2+384(4≤x≤6,且x取整数),
∵9>6,而当4≤x≤6时,W2随x的增大而增大,
∴当x=6时,w2最大=330万元;
∵450>330,
∴在前6个月中,第3月份食品加工厂的黑豆进货金额最大,最大金额为450万元;
(3)6月份的黑豆价格为:y2=-0.2×6+3.4=2.2(万元/吨),
进货量为:p2=30×6-30=150(吨),
由题意,得2.2(1-a%)×150(1+2a%)=363,
整理,得a2-50a+500=0,
解得a=25±5
| 5 |
∵
| 5 |
∴a≈14或a≈36.
∵所求为最大整数值,
∴a取36.
答:a的最大整数值为36.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目



 落在点D的位置.
落在点D的位置.
