题目内容
在直角梯形ABCD中,AB∥DC,AB⊥BC,∠A=60°,AB=2CD,E、F分别为AB、AD的中点,连接EF、EC、BF、CF;
(1)判断四边形AECD的形状;(不需要说理)
(2)△CDF与△BEF全等吗?请说明理由.

(1)判断四边形AECD的形状;(不需要说理)
(2)△CDF与△BEF全等吗?请说明理由.

(1)平行四边形.理由如下:
∵AB=2CD,E为AB的中点,即AB=2AE=2BE,
∴AE=CD,
∵AB∥DC,
∴四边形AECD为平行四边形.
(2)全等.理由如下:
连接DE,
∵AB=2CD,E为AB的中点,即AB=2AE=2BE,
∴EB=CD,
∵EB∥DC,
∴四边形EBCD为平行四边形.
∵∠ABC=90°,
∴平行四边形BCDE是矩形,所以∠AED=90°,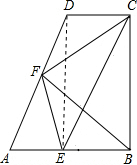
又∵F是AD的中点,
∴EF=DF=AF=
AD,
因为∠A=60°,
得△AEF是等边三角形,
从而∠BEF=∠CDF=120°,
在△CDF与△BEF中,
∵
,
∴△CDF≌△BEF(SAS).
∵AB=2CD,E为AB的中点,即AB=2AE=2BE,
∴AE=CD,
∵AB∥DC,
∴四边形AECD为平行四边形.
(2)全等.理由如下:
连接DE,
∵AB=2CD,E为AB的中点,即AB=2AE=2BE,
∴EB=CD,
∵EB∥DC,
∴四边形EBCD为平行四边形.
∵∠ABC=90°,
∴平行四边形BCDE是矩形,所以∠AED=90°,

又∵F是AD的中点,
∴EF=DF=AF=
| 1 |
| 2 |
因为∠A=60°,
得△AEF是等边三角形,
从而∠BEF=∠CDF=120°,
在△CDF与△BEF中,
∵
|
∴△CDF≌△BEF(SAS).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




