Question

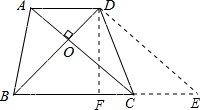
如图，已知等腰梯形ABCD中，AD∥BC，AC⊥BD，AD+BC=16cm，求梯形ABCD的面积．

Answer 1

过点D作DE∥AC交BC的延长线于点E，
∵AD∥BC（已知），
即AD∥CE，
∴四边形ACED是平行四边形，
∴AD=CE，AC=DE，
在等腰梯形ABCD中，AC=DB，
∴DB=DE（等量代换），
∵AC⊥BD，AC∥DE，
∴DB⊥DE，
∴△BDE是等腰直角三角形，
作DF⊥BC于F，
则DF=

1

2

BE=8，
S_梯形ABCD=

1

2

（AD+BC）•DF=

1

2

×16×8=64，
答：梯形ABCD的面积是64．