Question

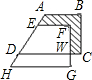
如图，在梯形ABCD中，AB∥CD，∠BCD=90°，BD平分∠ABC．
（1）求证：DC=BC；
（2）E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论；
（3）在（2）的条件下，当BE：CE=1：2，∠BEC=135°时，求

BE

BF

的值．

Answer 1

（1）证明：∵BD平分∠ABC，
∴∠ABD=∠CBD，
∵AB∥CD，
∴∠ABD=∠BDC，
∴∠CBD=∠BDC，
∴DC=BC；

（2）等腰直角三角形．
理由如下：在△DEC和△BFC中，

DE=BF ∠EDC=∠FBC DC=BC

，
∴△DEC≌△BFC（SAS），
∴CE=CF，∠ECD=∠BCF，
∴∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=90°，
即△ECF是等腰直角三角形；

（3）∵BE：CE=1：2，
∴设BE=k，CE=2k，
则EF=

2

CE=2

2

k，
∵∠BEC=135°，∠CEF=45°，
∴∠BEF=135°-45°=90°，
∴BF=

k2+(2 2 k)2

=3k，
∴

BE

BF

=

k

3k

=

1

3

．