题目内容
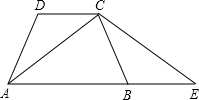
如图，等腰梯形ABCD中，AD∥BC，DE⊥BC，BD⊥DC，垂足分别为E，D，DE=3，BD=5，则腰长AB=______．
∵DE=3，BD=5，DE⊥BC，
∴BE=
=
=4，
又∵BD⊥DC，
∴tan∠CBD=
=
，
即
=
，
解得CD=
，
∵梯形ABCD是等腰梯形，AD∥BC，
∴AB=CD=
．
故答案为：
．
∴BE=
| BD2-DE2 |
| 52-32 |
又∵BD⊥DC，
∴tan∠CBD=
| CD |
| BD |
| DE |
| BE |
即
| CD |
| 5 |
| 3 |
| 4 |
解得CD=
| 15 |
| 4 |
∵梯形ABCD是等腰梯形，AD∥BC，
∴AB=CD=
| 15 |
| 4 |
故答案为：
| 15 |
| 4 |
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
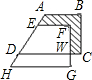
），点P（t，0）是线段OC上一点，设四边形ABCP的面积为S．