Question

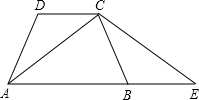
等腰梯形ABCD中，AD∥BC，E、F、G、H分别是AD、BE、BC、CE的中点．
试探究：
（1）四边形EFGH的形状；
（2）若BC=2AD，且梯形ABCD的面积为9，求四边形EFGH的面积．

Answer 1

（1）∵梯形ABCD是等腰梯形，
∴AB=CD，∠A=∠D（等腰梯形的两腰相等，在同一底边上的两内角相等），
又∵AE=DE，
∴△ABE≌△DCE（SAS）．
∴BE=CE（全等三角形的对应边相等）．
又∵EF=

1

2

EB，EH=

1

2

EC，
∴EF=EH．
∵G、F、H分别是BC、BE、CE的中点，
∴GF∥CE，GH∥BE（三角形中位线定理）．
∴四边形EFGH是平行四边形（平行四边形的定义）．
∴四边形EFGH是菱形（有一组邻边相等的平行四边形是菱形）．

（2）∵BE=CE，G为BC中点，
∴EG⊥BC（等腰三角形的三线合一）．
∴EG为梯形ABCD的高．
∵S_梯形=

1

2

（AD+BC）×EG=9，BC=2AD，
∴

1

2

（

1

2

BC+BC）×EG=9，
∴BC•EG=12．
∵F、H分别是BE、CE的中点，
∴FH=

1

2

BC．
∴S_菱形EFGH=

1

2

FH•EG=

1

2

×

1

2

×BC•EG=3．