题目内容
| |||||
答案：
解析：
解析：
|
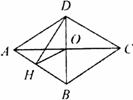
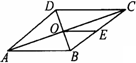
证明：∵四边形ABCD是菱形， ∴OD＝OB，∠COD＝90°． 又∵DH⊥AB，∴OH＝OB， ∴∠OHB＝∠OBH． ∵AB∥CD， ∴∠OBH＝∠ODC． ∴∠OHB＝∠ODC． 在Rt△COD中，∠ODC＋∠DCO＝90°， 在Rt△DHB中，∠DHO＋∠OHB＝90°， ∴∠DHO＝∠DCO． |
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
| |||||
，
，
)
| |||||||||||||||
．