Question

如图，在△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC．设MN交∠ACB的平分线于点E，交△ACB的外角∠ACD的平分线于点F． (1)求证：OE＝OF． (2)若CE＝12，CF＝5，求OC的长． (3)连接AE、AF，当点O在AC边上运动到什么位置时，四边形AECF是矩形？并说明理由．

Answer 1

答案：
解析：

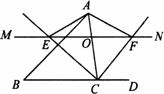
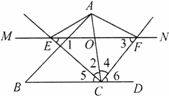
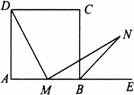
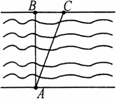
(1)证明：∵MN交∠ACB的平分线于点E，交∠ACD的平分线于点F， 　　∴∠2＝∠5，4＝∠6． 　　∵MN∥BC， 　　∴∠1＝∠5，3＝∠6， 　　∴∠1＝∠2，∠3＝∠4， 　　∴EO＝CO，FO＝CO， 　　∴OE＝OF． 　　(2)解：∵∠2＝∠5，∠4＝∠6， 　　∴∠2＋∠4＝∠5＋∠6＝90°． 　　∵CE＝12，CF＝5， 　　∴， 　　又∵O为EF的中点，∴． 　　(3)解：当点O在AC边上运动到AC的中点时，四边形AECF是矩形． 　　证明：当O为AC的中点时，AO＝CO， 　　又EO＝FO， 　　∴四边形AECF是平行四边形． 　　又∵∠ECF＝90°， 　　∴平行四边形AECF是矩形．