题目内容
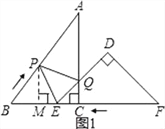
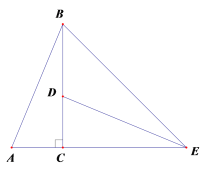
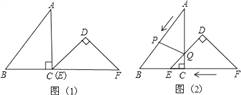
【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
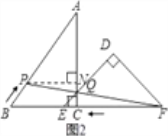
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
【答案】(1)2s;(2)存在,![]() cm2;(3)存在,t=1s
cm2;(3)存在,t=1s
【解析】试题分析:
(1)由已知条件先证△ECQ中,CQ=EC=t,由此可得AQ=8-t,由勾股定理可得AB=10,由此可得AP=AB-BP=10-2t,若点A在PQ的垂直平分线上,则有AP=AQ,由此可得关于t的方程,解此方程即可得到所求的t的值;
(2)如图1,过点P作PM⊥BE,交BE于M,由sinB=![]() =
=![]() ,可得
,可得![]() ,由此可得PM=
,由此可得PM=![]() ,再由S四边形APEC=S△ABC-S△APE即可用含t的式子表达出四边形APEC的面积了,再将所得表达式配方,即可求得当t为何值时,四边形ABEC的面积最小了;
,再由S四边形APEC=S△ABC-S△APE即可用含t的式子表达出四边形APEC的面积了,再将所得表达式配方,即可求得当t为何值时,四边形ABEC的面积最小了;
(3)如图2,假设在某一时刻,点P、F、Q在同一直线上,此时,过点P作PN⊥AC于点N,则易得△PAN∽△BAC,由此可得![]() ,即
,即![]() ,则可得PN=6﹣
,则可得PN=6﹣![]() t ,AN=8﹣
t ,AN=8﹣![]() t,这样即可得到NQ=8﹣t﹣(8﹣
t,这样即可得到NQ=8﹣t﹣(8﹣![]() )=
)=![]() ,再证△QCF∽△QNP从而可得
,再证△QCF∽△QNP从而可得![]() ,即
,即![]() ,由此即可解得所求的t的值了.
,由此即可解得所求的t的值了.
试题解析:
(1)∵点A在线段PQ的垂直平分线上,
∴AP=AQ;
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°;
∴∠DEF=∠EQC;
∴CE=CQ;
由题意知:CE=t,BP=2t,
∴CQ=t;
∴AQ=8﹣t;
在Rt△ABC中,由勾股定理得:AB=10cm;
则AP=10﹣2t;
∴10﹣2t=8﹣t;
解得:t=2;
答:当t=2s时,点A在线段PQ的垂直平分线上;
(2)如下图1,过P作PM⊥BE,交BE于M,
∴∠BMP=90°;
在Rt△ABC和Rt△BPM中,sinB=![]() =
=![]() ,
,
∴![]() ,
,
∴PM=![]() ,
,
∵BC=6cm,CE=t,
∴BE=6﹣t,
∴y=S△ABC﹣S△BPE
=![]() BCAC﹣
BCAC﹣![]() BEPM
BEPM
=![]() ×6×8﹣
×6×8﹣![]() (6﹣t)×
(6﹣t)×![]()
=![]()
=![]() ,
,
∵![]() ,
,
∴抛物线开口向上;
∴当t=3时,y最小=![]() ;
;
答:当t=3s时,四边形APEC的面积最小,最小面积为![]() cm2.
cm2.
(3)假设存在某一时刻t,使点P、Q、F三点在同一条直线上;
如图2,过P作PN⊥AC,交AC于N
∴∠ANP=∠ACB=∠PNQ=90°;
∵∠PAN=∠BAC,
∴△PAN∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴PN=6﹣![]() t ,AN=8﹣
t ,AN=8﹣![]() t,
t,
∵NQ=AQ﹣AN,
∴NQ=8﹣t﹣(8﹣![]() )=
)=![]() ,
,
∵∠ACB=90°,B、C、E、F在同一条直线上,
∴∠QCF=90°,∠QCF=∠PNQ;
∵∠FQC=∠PQN,
∴△QCF∽△QNP;
∴![]() ,即
,即![]() ;
;
∵0<t<4.5,
∴![]() ,
,
解得:t=1;
答:当t=1s,点P、Q、F三点在同一条直线上.