题目内容
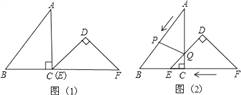
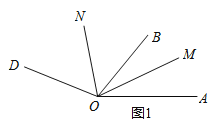
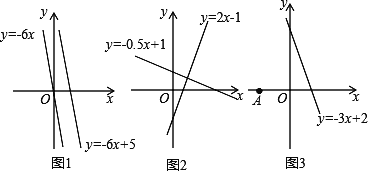
【题目】材料一：如图1，由课本91页例2画函数y＝﹣6x与y＝﹣6x+5可知，直线y＝﹣6x+5可以由直线y＝﹣6x向上平移5个单位长度得到由此我们得到正确的结论一：在直线L1：y=K1x+b1与直线L2：y=K2x+b2中，如果K1=K2 且b1≠b2 ，那么L1∥L2，反过来，也成立．
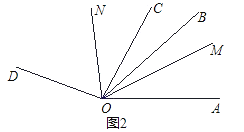
材料二：如图2，由课本92页例3画函数y＝2x﹣1与y＝﹣0.5x+1可知，利用所学知识一定能证出这两条直线是互相垂直的．由此我们得到正确的结论二：在直线L1：y=k1x+b1 与L2：y=k2x+b2 中，如果k1·k2=-1那么L1⊥L2，反过来，也成立
应用举例
已知直线y＝﹣
x+5与直线y＝kx+2互相垂直，则﹣k＝﹣1．所以k＝6
解决问题
(1)请写出一条直线解析式______，使它与直线y＝x﹣3平行．
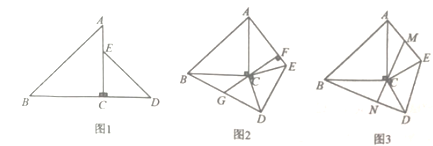
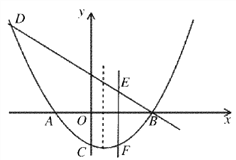
(2)如图3，点A坐标为(﹣1，0)，点P是直线y＝﹣3x+2上一动点，当点P运动到何位置时，线段PA的长度最小？并求出此时点P的坐标．
【答案】（1）y＝x；（2）当线段PA的长度最小时，点P的坐标为
.
【解析】
（1）由两直线平行可得出k1＝k2＝1、b1≠b2＝﹣3，取b1＝0即可得出结论；
（2）过点A作AP⊥直线y＝﹣3x+2于点P，此时线段PA的长度最小，由两直线平行可设直线PA的解析式为y＝
x+b，由点A的坐标利用待定系数法可求出直线PA的解析式，联立两直线解析式成方程组，再通过解方程组即可求出：当线段PA的长度最小时，点P的坐标．
.解：（1）∵两直线平行，
∴k1＝k2＝1，b1≠b2＝﹣3，
∴该直线可以为y＝x．
故答案为：y＝x．
（2）过点A作AP⊥直线y＝﹣3x+2于点P，此时线段PA的长度最小，如图所示．
∵直线PA与直线y＝﹣3x+2垂直，
∴设直线PA的解析式为y＝x+b．
∵点A（﹣1，0）在直线PA上，
∴×（﹣1）+b＝0，解得：b＝，
∴直线PA的解析式为y＝x+．
联立两直线解析式成方程组，得：
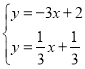，解得：
．
∴当线段PA的长度最小时，点P的坐标为（
，）．
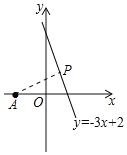
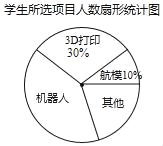
名校课堂系列答案【题目】初一（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查（每名学生分别选一个活动项目），并根据调查结果列出统计表，绘制成扇形统计图．
男、女生所选项目人数统计表
项目 | 男生（人数） | 女生（人数） |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题：
（1）m=_____，n=_____；
（2）扇形统计图中机器人项目所对应扇形的圆心角度数为_____°；
（3）从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法（画树状图或列表）求所选取的2名学生中恰好有1名男生、1名女生的概率．
【题目】某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）
甲 | 乙 | |
进价（元/件） | 22 | 30 |
售价（元/件） | 29 | 40 |
（1）该超市购进甲、乙两种商品各多少件？
（2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙商品是按原价打几折销售？
