题目内容
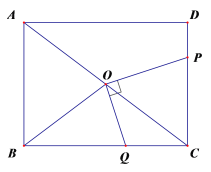
【题目】如图,在长方形ABCD中,AB=6,BC=8,点O在对角线AC上,且OA=OB=OC,点P是边CD上的一个动点,连接OP,过点O作OQ⊥OP,交BC于点Q.
(1)求OB的长度;
(2)设DP= x,CQ= y,求y与x的函数表达式(不要求写自变量的取值范围);
(3)若![]() OCQ是等腰三角形,求CQ的长度.
OCQ是等腰三角形,求CQ的长度.
【答案】(1)5;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.
【解析】
(1)利用勾股定理先求出AC的长,继而根据已知条件即可求得答案;
(2)延长QO交AD于点E,连接PE、PQ ,先证明△AEO≌△CQO,从而得OE=OQ,AE=CQ=y,由垂直平分线的性质可得PE=PQ,即![]() ,在Rt⊿EDP中,有
,在Rt⊿EDP中,有![]() ,在Rt⊿PCQ中,
,在Rt⊿PCQ中,![]() ,继而可求得答案;
,继而可求得答案;
(3)分CQ=CO,OQ=CQ,OQ=OC三种情况分别进行讨论即可求得答案.
(1)∵四边形ABCD是长方形,
∴∠ABC=90°,
∴![]() ,
,
∴OB=OA=OC=![]() ;
;
(2)延长QO交AD于点E,连接PE、PQ ,
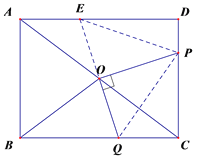
∵四边形ABCD是长方形,
∴CD=AB=6,AD=BC=8,AD//BC,
∴∠AEO=∠CQO,
在△COQ和△AOE中,
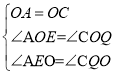 ,
,
∴△AEO≌△CQO(SAS),
∴OE=OQ,AE=CQ=y,
∴ED=AD-AE=8-y,
∵OP⊥OQ,
∴OP垂直平分EQ,
∴PE=PQ,
∴![]() ,
,
∵PD=x,
∴CP=CD-CP=6-x,
在Rt⊿EDP中,![]() ,
,
在Rt⊿PCQ中,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)分三种情况考虑:
①如图,若CQ=CO时,此时CQ=CO=5;
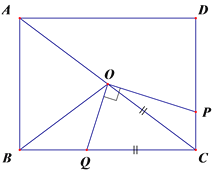
②如图,若OQ=CQ时,作OF⊥BC,垂足为点F,
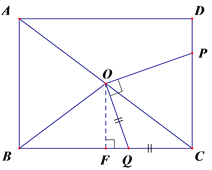
∵OB=OC,OF⊥BC,
∴BF=CF=![]() BC=4,
BC=4,
∴![]() ,
,
∵OQ=CQ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
③若OQ=OC时,此时点Q与点B重合,点P在DC延长线上,此情况不成立,
综上所示,当![]() 或
或![]() 时,⊿OCQ是等腰三角形.
时,⊿OCQ是等腰三角形.