题目内容
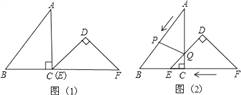
【题目】如图,![]() ABC中,∠ACB=90°,∠ABC=22.5°,将
ABC中,∠ACB=90°,∠ABC=22.5°,将![]() ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
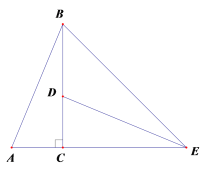
①DE⊥AB ②∠BCE是旋转角 ③∠BED=30° ④![]() BDE与
BDE与![]() CDE面积之比是
CDE面积之比是![]() :1
:1
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
延长ED交AB于点F,连接AD,根据直角三角形两锐角互余可得∠BAC=67.5°,根据旋转的性质可得∠BCE=∠ACD=90°,∠BCE是旋转角,CD=AC,CE=CB,∠CED=交ABC=22.5°,继而可得 ∠AFE=90°,即DE⊥AB,可得∠DAC=∠ADC=45°,∠CBE=∠CEB=45°,AD=![]() ,从而可得 ∠BAD=22.5°,∠BED=22.5°,从而可得 BD=AD=
,从而可得 ∠BAD=22.5°,∠BED=22.5°,从而可得 BD=AD=![]() CD,得到
CD,得到![]() BDE与
BDE与![]() CDE面积之比是
CDE面积之比是![]() :1,据此即可得出正确答案.
:1,据此即可得出正确答案.
延长ED交AB于点F,连接AD,
∵∠ACB=90°,∠ABC=22.5°,
∴∠BAC=90°-∠ABC=67.5°,
∵将![]() ABC 绕着点.顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,
ABC 绕着点.顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,
∴∠BCE=∠ACD=90°,∠BCE是旋转角,CD=AC,CE=CB,∠CED=∠ABC=22.5°,
∴∠CED+∠BAC=90°,∴∠AFE=90°,即DE⊥AB,
∵∠BCE=∠ACD=90°,CD=AC,CE=CB,
∴∠DAC=∠ADC=45°,∠CBE=∠CEB=45°,AD=![]() ,
,
∴∠BAD=67.5°-45°=22.5°,∠BED=∠BEC-∠DEC=45°-22.5°=22.5°,
∴∠BAD=∠ABD,
∴BD=AD=![]() CD,
CD,
∴![]() BDE与
BDE与![]() CDE面积之比是BD:CD=
CDE面积之比是BD:CD=![]() :1,
:1,
综上可知,正确的是①②④,共3个,
故选C.


【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?