题目内容
【题目】问题提出:
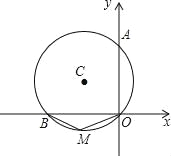
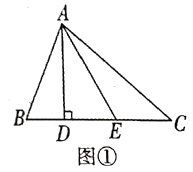
(1)如图①在![]() 中,
中,![]() 是
是![]() 边
边![]() 的高,点
的高,点![]() 是
是![]() 上任意一点,若
上任意一点,若![]() 则
则![]() 的最小值为_ ;
的最小值为_ ;
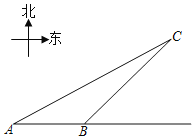
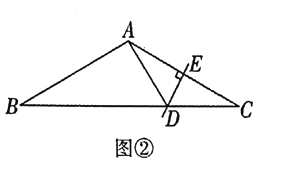
(2)如图②,在等腰![]() 中,
中,![]() 是
是![]() 的垂直平分线,分别交
的垂直平分线,分别交![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的周长;
的周长;
问题解决:
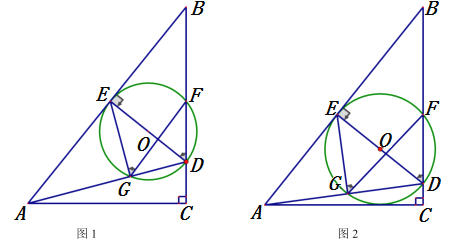
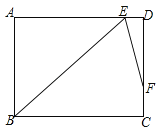
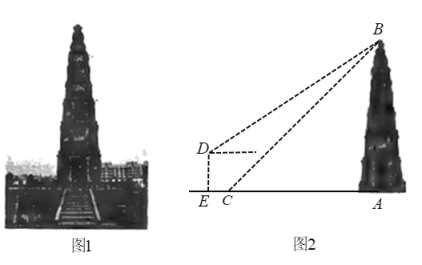
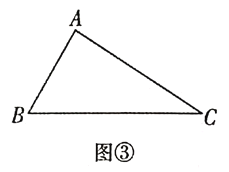
(3)如图③,某公园管理员拟在园内规划一个![]() 区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路
区域种植花卉,且为方便游客游览,欲在各顶点之间规划道路![]() 和
和![]() ,满足
,满足![]() 点
点![]() 到
到![]() 的距离为
的距离为![]() .为了节约成本,要使得
.为了节约成本,要使得![]() 之和最短,试求
之和最短,试求![]() 的最小值(路宽忽略不计).
的最小值(路宽忽略不计).
【答案】(1)3;(2)![]() ;(3)
;(3)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)根据直线外一点与直线上的点的所有连线中,垂线段最短即可求解;
(2)由已知和等腰三角形的性质得出![]() ,根据垂直平分线的性质和含30度角的直角三角形的性质可依次得出
,根据垂直平分线的性质和含30度角的直角三角形的性质可依次得出![]() ,
,![]() ,利用勾股定理求出AB,即可求得
,利用勾股定理求出AB,即可求得![]() 的周长;
的周长;
(3)延长![]() 到点
到点![]() ,使得
,使得![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,则
,则![]() 的最小值即为
的最小值即为![]() 的最小值;通过角的计算可得
的最小值;通过角的计算可得![]() ,可得点
,可得点![]() 在弦
在弦![]() 所对的劣弧上;过点
所对的劣弧上;过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
由![]() 即可求得结果.
即可求得结果.
解:(1)∵![]() 是
是![]() 边
边![]() 的高,
的高,![]() ,
,
∴![]() ,点D到直线BC的距离为3,
,点D到直线BC的距离为3,
∵点![]() 是
是![]() 上任意一点,
上任意一点,
∴![]() ,即
,即![]() ,
,
∴![]() 的最小值为3,
的最小值为3,
故答案为:3.
(2)![]() ,
,
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
![]()
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的周长
的周长![]() ;
;
(3)如图,延长![]() 到点
到点![]() ,使得
,使得![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 的最小值即为
的最小值即为![]() 的最小值,
的最小值,
![]()
![]() ,
,
以![]() 为斜边向下作等腰直角三角形
为斜边向下作等腰直角三角形![]() ,则
,则![]() ,
,
以点![]() 为圆心
为圆心![]() 为半径作
为半径作![]() ,F为圆上任意一点,则
,F为圆上任意一点,则![]() ,
,
∵![]() ,
,
![]() 点
点![]() 在弦
在弦![]() 所对的劣弧上,
所对的劣弧上,
如图,过点![]() 作
作![]() 于
于![]() 过点
过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() ,
,
设![]() 则
则![]()
则![]() ,即
,即![]()
解得:![]() ,则
,则![]() ,
,
![]() 的最小值为
的最小值为![]() ,
,
![]() 的最小值为
的最小值为![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目