Question

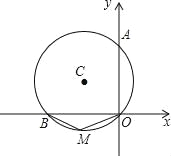
【题目】如图，⊙C 经过原点且与两坐标轴分别交于点 A 与点 B，点 B 的坐标为（﹣，0），M 是圆上一点，∠BMO=120°．⊙C 圆心 C 的坐标是_____．

Answer 1

【答案】（，）

【解析】

连接AB，OC，由圆周角定理可知AB为⊙C的直径，再根据∠BMO=120°可求出∠BAO以及∠BCO的度数，在Rt△COD中，解直角三角形即可解决问题；

连接AB，OC，

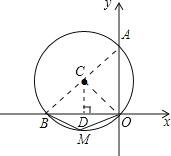
∵∠AOB=90°，

∴AB为⊙C的直径，

∵∠BMO=120°，

∴∠BAO=60°，

∴∠BCO=2∠BAO=120°，

过C作CD⊥OB于D，则OD=OB，∠DCB=∠DCO=60°，

∵B（-，0），

∴BD=OD=

在Rt△COD中．CD=ODtan30°=，

∴C（-，），

故答案为：C（-，）．