题目内容
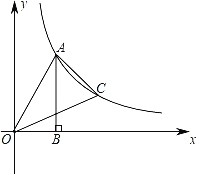
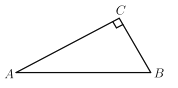
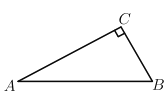
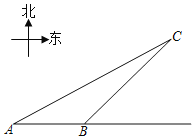
【题目】如图,我市某景区内有一条自西向东的笔直林荫路经过景点A、B,现市政决定开发景点C,经考察人员测量,景点A位于景点C的在南偏西60°方向,景点B位于景点C的西南方向,A、B两景点之间相距380米,现准备由景点C向该林萌路修建一条距离最短的公路,不考虑其它因素,求出这条公路的长?(结果精确到0.1,参考数据:![]() ≈1.732)
≈1.732)
【答案】这条公路的长约为519.1米.
【解析】
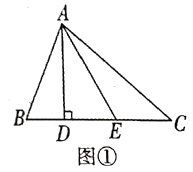
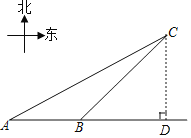
过点C作CD⊥AB于点D,由题意可得,∠DCA=60°,∠DCB=45°,AB=380,然后根据三角函数即可求出CD的长,进而可得距离最短的公路的长.
解:如图,过点C作CD⊥AB于点D,
由题意可知:
∠DCA=60°,∠DCB=45°,AB=380,
∴在Rt△BCD中,CD=BD,
在Rt△ACD中,tan∠DCA=![]() ,
,
∴tan60°=![]() =
=![]() ,
,
∴CD=190![]() +190≈519.1(米).
+190≈519.1(米).
答:这条公路的长约为519.1米.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】某中学抽取了40 名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数 /人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |

(1)求频数分布表中的m的值
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全统计图.
(3) 已知 该校有2000名学生,请你估计该校平均每周课外阅读时间在![]() 范围内的学生人数
范围内的学生人数
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.