题目内容
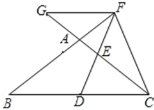
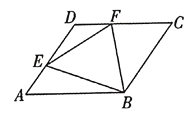
【题目】如图,菱形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 上一动点(不与
上一动点(不与![]() 重合),点
重合),点![]() 是
是![]() 上一动点,
上一动点,![]() 则
则![]() 面积的最小值为____.
面积的最小值为____.
【答案】![]()
【解析】
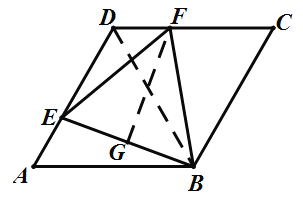
连结BD,利用SAS证得△BDF≌△BAE,可得△BEF是等边三角形,当BE⊥AD时面积最小即可求解.
解:连接BD,
∵菱形ABCD边长为4,∠BAD=60°,
∴AB=BC=CD=AD=4,∠BAD=∠BCD=60°,
∴△ABD与△BCD为等边三角形,
∴∠FDB=∠EAB=∠ABD =60°,BA=BD,
∵AE+CF=4,DF+CF=CD=4,
∴AE=DF,
在△BDF和△BAE中,
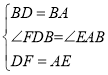 ,
,
∴△BDF≌△BAE(SAS),
∴BE=BF,∠ABE=∠DBF,
∴![]() ,即∠EBF=∠ABD=60°,
,即∠EBF=∠ABD=60°,
∴△BEF是等边三角形,
∴当BE⊥AD时,△BEF的面积最小,此时点E为AD的中点,
∴![]() ,则
,则![]() ,
,
过点F作FG⊥BE于点G,则点G为BE中点,
∴![]() ,则
,则![]() ,
,
∴△BEF面积的最小值![]() ,
,
故答案为:![]() .
.

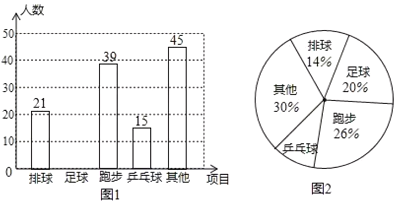
【题目】某中学抽取了40 名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数 /人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |

(1)求频数分布表中的m的值
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全统计图.
(3) 已知 该校有2000名学生,请你估计该校平均每周课外阅读时间在![]() 范围内的学生人数
范围内的学生人数
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.